Will man einen Bruch erweitern, muss man Zähler und Nenner mit derselben Zahl multiplizieren. Weil sich Zähler und Nenner dabei um denselben Faktor vergrößern, ändert sich der Wert des Bruches nicht (das Erweitern eines Bruches entspricht einer Multiplikation mit einem Bruch, der den Wert „1“ hat). Die umgekehrte Operation zum Erweitern von Brüchen ist das Kürzen von Brüchen. Für eine noch ausführlichere Hilfe besteht immer die Möglichkeit einer Mathe Nachhilfe.
Die allgemeine Formeln, um Brüche zu erweitern, lautet:
In der folgenden Tabelle werden mehrere Brüche gezeigt. Sie haben alle unterschiedliche Zähler und Nenner. Ihr Wert ist aber derselbe. Die oberen vier Brüche stellen dabei eine Erweiterung des untersten Bruchs (1/2) dar:
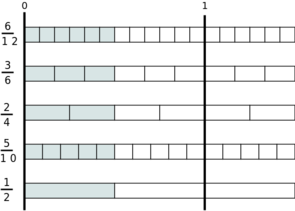
Beispiele zum Erweitern von Brüchen
Die folgenden Beispiele zeigen, wir sich Brüche erweitern lassen:
Im ersten Beispiel wird der Bruch 3/4 mit 2 erweitert, im zweiten 5/7 mit 9 und in den letzten beiden Beispielen wird zweimal der Bruch 1/12 erweitert, einmal mit 12 und einmal mit 6.
Das folgende Beispiel zeigt, was passiert, wenn man einen Bruch zweimal erweitert. Er hat danach dieselbe Darstellung, als hätte man ihn direkt mit dem Produkt der beiden Zahlen erweitert:
Der Grund hierfür liegt im Assoziativgesetz der Multiplikation
Wozu muss man Brüche erweitern?
Zähler und Nenner werden beim Erweitern größer. Die Bruchrechnung wird dadurch eher komplizierter. Warum soll man Brüche also überhaupt erweitern?
Der Grund liegt darin, dass man zwei Brüche nur dann vergleichen, addieren oder subtrahieren kann, wenn sie denselben Nenner haben. Deshalb muss man Brüche häufig gleichnamig machen. Zwei gleichnamige Brüche sind Brüche, die denselben Nenner haben. Falls man die Brüche nicht auf denselben Nennen bringen kann, indem man einen von ihnen kürzt, muss man die Brüche erweitern. Die einfachste Möglichkeit, zwei Brüche gleichnamig zu machen, ist es, sie jeweils um den Nenner des anderen Bruchs zu erweitern.
Das folgende Beispiel zeigt, wie man die Brüche 3/4 und 1/5 gleichnamig macht. Dabei wird der erste Bruche mit 5, der zweite mit 4 erweitert. Anschließend haben beide denselben Nenner:
