Loki, Autor bei Formelsammlung Mathe

Von Spielspaß bis Spielsucht: Alles, was du über Online Glücksspiel in Deutschland wissen musst

Online Glücksspiel hat in den letzten Jahren in Deutschland stark zugenommen und ist für viele Menschen zu einem beliebten Freizeitvergnügen geworden. Doch wie sieht die rechtliche Situation in Deutschland aus? Welche Vor- und Nachteile gibt es beim Online Glücksspiel? Kann man gewinnen oder gewinnt am Ende die Bank?

Definition von Online Glücksspiel

Unter Online Glücksspiel versteht man das Spielen von Glücksspielen im Internet. Hierzu gehören beispielsweise Online Casinos, Poker-Plattformen oder Sportwetten-Anbieter, bei denen man gegen andere Spieler oder gegen den Anbieter selbst spielt. Die Teilnahme am Online Glücksspiel erfolgt über eine Internetverbindung und kann von jedem Ort aus erfolgen, solange eine Verbindung zum Internet besteht.

Rechtliche Situation

Die rechtliche Situation von Online Glücksspiel in Deutschland ist komplex und von Bundesland zu Bundesland unterschiedlich. Grundsätzlich ist das Online Glücksspiel in Deutschland nur erlaubt, wenn der Anbieter eine gültige Lizenz besitzt. Diese Lizenz wird von den Bundesländern vergeben und ist an strenge Auflagen gebunden.

Der Glücksspielstaatsvertrag regelt die Rahmenbedingungen für das Glücksspiel in Deutschland. Zuletzt gab es 2021 Änderungen. Allerdings haben die Bundesländer die Möglichkeit, eigene Regelungen zu treffen, was zu unterschiedlichen Regelungen in den einzelnen Bundesländern führt. Illegale Anbieter von Online Glücksspielen sind strafbar und können mit hohen Geldstrafen oder sogar Freiheitsstrafen belegt werden.

Legale Anbieter finden

Um legale Anbieter von Online Glücksspiel in Deutschland zu finden, sollte man auf folgende Punkte achten:

Lizenz: Ein seriöser Anbieter besitzt eine gültige Lizenz, die von einem deutschen Bundesland ausgestellt wurde. Diese Lizenz sollte auf der Webseite des Anbieters einsehbar sein.
Sicherheit: Der Anbieter sollte über eine sichere Verschlüsselung (SSL) verfügen, um die Angaben der Spieler zu schützen. Außerdem sollte der Anbieter verantwortungsvolles Spielen fördern und Maßnahmen gegen Spielsucht anbieten.
Spieleangebot: Ein seriöser Anbieter bietet eine breite Auswahl an Spielen von renommierten Herstellern an. Dabei sollten auch beliebte Klassiker wie Roulette, Blackjack oder Spielautomaten vorhanden sein.
Zahlungsmethoden: Der Anbieter sollte eine sichere und bequeme Auswahl an Zahlungsmethoden anbieten, wie zum Beispiel Kreditkarte, Banküberweisung oder E-Wallets.
Kundenservice: Ein guter Kundenservice ist wichtig, um bei Fragen oder Problemen schnell und kompetent Hilfe zu erhalten. Der Anbieter sollte einen Kundenservice per E-Mail, Telefon oder Live-Chat anbieten.

Vor- und Nachteile von Online Glücksspiel

Das Online Glücksspiel bietet viele Vorteile, wie zum Beispiel eine breite Auswahl an Spielen und bequemen Zugang von jedem Ort aus. Allerdings gibt es auch Risiken und Gefahren, wie die Spielsucht und betrügerische Anbieter. In diesem Abschnitt werden wir uns genauer mit den Vor- und Nachteilen von Online Glücksspiel auseinandersetzen.

Vorteile für Spieler

Das Online Glücksspiel bietet eine Vielzahl von Vorteilen für Spieler. Zum einen ist es sehr bequem, da man jederzeit und von jedem Ort aus spielen kann, solange eine Internetverbindung besteht. Es entfällt somit der Weg in eine Spielhalle oder ein Casino. Zum anderen bietet das Online Glücksspiel oft eine breitere Auswahl an Spielen als herkömmliche Spielstätten. Spieler können aus einer Vielzahl von Spielautomaten, Tischspielen und Live-Dealer-Spielen wählen. Ein weiterer Vorteil ist die Möglichkeit, Boni und Promotionen zu nutzen, die von Online Casinos und anderen Anbietern angeboten werden. Diese können das Spielvergnügen erhöhen und die Gewinnchancen verbessern.

Risiken und Gefahren von Online Glücksspiel

Das Online Glücksspiel birgt auch einige Risiken und Gefahren. Eine der größten Gefahren ist die Spielsucht. Durch die ständige Verfügbarkeit und den einfachen Zugang zum Glücksspiel können Spieler schnell in eine Abhängigkeit geraten. Auch die Anonymität des Internets kann dazu führen, dass Spieler ihre Grenzen überschreiten und mehr Geld ausgeben, als sie eigentlich können oder sollten. Ein weiteres Risiko sind betrügerische Anbieter, die keine gültige Lizenz besitzen und Spieler um ihr Geld bringen. Es ist daher wichtig, nur bei seriösen Anbietern zu spielen und verantwortungsvoll mit dem Glücksspiel umzugehen.

Verantwortungsvoller Umgang mit Online-Glücksspiel

Ein verantwortungsvoller Umgang mit Online-Glücksspiel ist von großer Bedeutung, um die Risiken und Gefahren des Glücksspiels zu minimieren. Dazu gehört, dass man sich über die eigenen Grenzen und das eigene Budget im Klaren ist und diese auch einhält. Es ist wichtig, sich ein Limit für das Spielen zu setzen und dieses auch einzuhalten, um nicht in eine Abhängigkeit zu geraten.

Zudem sollte man sich nur bei seriösen Anbietern registrieren, die eine gültige Lizenz besitzen und verantwortungsvolles Spielen fördern. Auch die Nutzung von Hilfsangeboten bei Spielsucht, wie zum Beispiel Beratungsstellen oder Selbsthilfegruppen, kann helfen, ein verantwortungsvolles Spielverhalten zu fördern.

Ebenso ist es wichtig, dass man sich bewusst macht, dass Glücksspiel in erster Linie ein Unterhaltungsangebot ist und nicht als Einkommensquelle genutzt werden sollte. Eine realistische Einschätzung der Gewinnchancen und Verlustmöglichkeiten kann dazu beitragen, dass man nicht in eine finanzielle Schieflage gerät.

Auch online sollte man seine Ausgaben im Blick behalten
Bildquelle: pixabay.com © besteonlinecasinos

Auch sollte man sich nicht unter Druck setzen lassen, beispielsweise durch Verlockungen zu höheren Einsätzen oder durch Verluste, die man wieder ausgleichen möchte. Ein verantwortungsvoller Umgang mit Online-Glücksspiel erfordert somit eine gewisse Selbstdisziplin und Achtsamkeit, um sich selbst und sein Umfeld zu schützen.

Fazit

Zusammenfassend kann gesagt werden, dass Online Glücksspiel in Deutschland eine wachsende Bedeutung hat und für viele Menschen zu einem beliebten Freizeitvergnügen geworden ist. Die rechtliche Situation ist jedoch komplex und von Bundesland zu Bundesland unterschiedlich. Um sicher und legal spielen zu können, sollten Spieler auf seriöse Anbieter achten, die eine gültige Lizenz besitzen und verantwortungsvolles Spielen fördern.

Das Online Glücksspiel bietet viele Vorteile, wie zum Beispiel eine breite Auswahl an Spielen und bequemen Zugang von jedem Ort aus. Allerdings gibt es auch Risiken und Gefahren, wie die Spielsucht und betrügerische Anbieter. Es ist daher wichtig, dass Spieler verantwortungsvoll mit dem Glücksspiel umgehen und sich über die Risiken und Gefahren informieren.

Insgesamt zeigt sich, dass das Online Glücksspiel in Deutschland eine wichtige Rolle spielt und auch in Zukunft weiter an Bedeutung gewinnen wird. Es bleibt abzuwarten, wie sich die rechtliche Situation in Deutschland weiter entwickeln und ob es in Zukunft eine einheitliche Regelung auf Bundesebene geben wird.

Zinseszins: Was ist das genau?

Der Zinseszins ist ein wichtiger Begriff in der Finanzwelt, der sich auf die Art und Weise bezieht, wie Zinsen auf Zinsen aufgebaut werden. Im Laufe der Zeit kann der Zinseszins enorme Auswirkungen auf die Höhe des Vermögens haben. In diesem Artikel werden wir näher auf das Konzept des Zinseszins eingehen und seine Bedeutung in der Finanzwelt erläutern.

Grundlegendes zum Zinseszins

Der Zinseszins ist das Ergebnis der Tatsache, dass Zinsen nicht nur auf das ursprünglich eingezahlte Kapital, sondern auch auf bereits erwirtschaftete Zinsen berechnet werden. Mit anderen Worten: Wenn Sie Geld anlegen und Zinsen verdienen, werden diese Zinsen in Ihrem Konto gutgeschrieben und zu Ihrem Gesamtkapital addiert. Anschließend werden die Zinsen auf das gesamte Kapital berechnet, einschließlich der bereits erhaltenen Zinsen. Dieses zusätzliche Geld, das durch den Zinseszins verdient wird, kann im Laufe der Zeit erheblich anwachsen.

Zinseszins – Beispiel

Wir werden die Zinsrechnung einmal veranschaulichen: Nehmen wir an, Sie haben 10.000 Euro auf einem Konto angelegt, das 5% Zinsen pro Jahr zahlt. Nach einem Jahr haben Sie 10.500 Euro, da Sie 5% Zinsen auf Ihr ursprüngliches Kapital von 10.000 Euro erhalten haben. Im zweiten Jahr erhalten Sie jedoch 5% Zinsen auf 10.500 Euro, nicht nur auf Ihr ursprüngliches Kapital von 10.000 Euro. Am Ende des zweiten Jahres haben Sie 11.025 Euro, da die zusätzlichen 25 Euro durch den Zinseszins verdient wurden.

Dieses Beispiel mag zunächst nicht besonders beeindruckend erscheinen, aber der Effekt des Zinseszins kann enorm sein, wenn er über lange Zeiträume hinweg arbeitet. Wenn Sie zum Beispiel 10.000 Euro in ein langfristiges Sparkonto mit 5% Zinsen pro Jahr investieren und 30 Jahre lang keine weiteren Einzahlungen vornehmen, würde Ihr Kapital auf über 43.000 Euro anwachsen. Das sind mehr als 30.000 Euro zusätzlich durch den Zinseszins.

Der Zinseszins und die Bedeutung der Zeit

Die Wirkung des Zinseszinses ist stark von der Zeit abhängig. Je länger das Kapital angelegt wird, desto stärker wirkt der Zinseszins. Dies liegt daran, dass das zusätzliche Kapital, das durch den Zinseszins verdient wird, mit der Zeit immer weiter anwächst. Dies führt dazu, dass sich das Kapital exponentiell vermehrt, wenn es über einen längeren Zeitraum hinweg arbeitet.

Ein weiterer Faktor, der die Auswirkungen des Zinseszins beeinflusst, ist die Höhe des Zinssatzes. Je höher der Zinssatz, desto größer sind die Auswirkungen des Zinseszins auf das Kapital. Wenn der Zinssatz jedoch sehr niedrig ist, kann es sehr lange dauern, bis der Zinseszins eine spürbare Wirkung hat.

Der Zinseszins in der Praxis

Der Zinseszins ist ein wichtiger Faktor in vielen Finanzprodukten und Investitionsstrategien. Einige der gebräuchlichsten Produkte, die den Zinseszins nutzen, sind Spar- und Anlagekonten, Rentenfonds, Aktien und Anleihen.

Spar- und Anlagekonten

Spar- und Anlagekonten sind eine der einfachsten Möglichkeiten, den Zinseszins zu nutzen. Bei diesen Konten erhalten Sie Zinsen auf das eingezahlte Kapital und die Zinsen, die Sie bereits erhalten haben. Je höher der Zinssatz und je länger das Kapital auf dem Konto bleibt, desto größer wird der Effekt des Zinseszins.

Rentenfonds

Rentenfonds sind Investmentfonds, die in Anleihen investieren. Diese Anleihen zahlen Zinsen und der Fondsmanager reinvestiert diese Zinsen in neue Anleihen. Dies führt zu einem Effekt des Zinseszins, der im Laufe der Zeit das Kapitalwachstum beschleunigt. Rentenfonds sind eine konservative Investition, die eine regelmäßige Einkommensquelle bieten kann.

Aktien

Aktien sind eine weitere Möglichkeit, den Zinseszins zu nutzen. Wenn Sie Aktien besitzen, können Sie Dividenden erhalten, die in der Regel jährlich oder vierteljährlich ausgezahlt werden. Diese Dividenden können reinvestiert werden, um zusätzliche Aktien zu kaufen, die wiederum Dividenden zahlen. Der Effekt des Zinseszins kann erheblich sein, insbesondere bei Unternehmen, die regelmäßig Dividenden zahlen und eine hohe Dividendenrendite haben.

Anleihen

Anleihen sind eine sichere und stabile Möglichkeit, den Zinseszins zu nutzen. Anleihen sind Schuldtitel, die von Unternehmen und Regierungen ausgegeben werden. Sie zahlen regelmäßig Zinsen und bei Fälligkeit wird das Kapital zurückgezahlt. Wenn Sie Anleihen besitzen, können Sie die Zinsen reinvestieren, um zusätzliche Anleihen zu kaufen. Der Effekt des Zinseszins kann erheblich sein, insbesondere bei langfristigen Anleihen.

Die Bedeutung des Zinseszins in der Altersvorsorge

Der Zinseszins ist auch ein wichtiger Faktor bei der Altersvorsorge. Durch das Sparen in einem Altersvorsorgeplan, wie beispielsweise einer betrieblichen Altersvorsorge oder einer privaten Rentenversicherung, können Sie den Effekt des Zinseszins nutzen, um Ihr Vermögen im Laufe der Zeit aufzubauen.

Bei einer betrieblichen Altersvorsorge oder einer privaten Rentenversicherung zahlen Sie regelmäßig Beiträge, die in Anlageprodukte wie Rentenfonds oder Anleihen investiert werden. Im Laufe der Zeit wächst Ihr Kapital durch den Effekt des Zinseszins exponentiell an. Wenn Sie dann in den Ruhestand gehen, können Sie regelmäßige Auszahlungen erhalten, die auf Ihrem angesammelten Vermögen basieren.

Die Bedeutung des Zinseszins bei Schulden

Der Zinseszins kann auch eine negative Auswirkung haben, wenn Sie Schulden haben. Wenn Sie Schulden haben, werden Zinsen auf die ausstehenden Beträge berechnet (z.B. bei einem Dispo am Girokonto). Diese Zinsen werden auf den ursprünglichen Betrag aufgeschlagen und erhöhen so den Gesamtbetrag, den Sie zurückzahlen müssen. Wenn Sie Ihre Schulden nicht schnell genug zurückzahlen, kann der Effekt des Zinseszins dazu führen, dass die Schulden exponentiell ansteigen und schwerer zu bewältigen werden.

Daher ist es wichtig, Schulden so schnell wie möglich zurückzuzahlen, um den Effekt des Zinseszins zu minimieren. Es kann auch hilfreich sein, Schulden mit höheren Zinssätzen zuerst abzuzahlen, um den Gesamteffekt des Zinseszins zu reduzieren.

Wenn Sie z.B. den Dispo am Girokonto nicht zeitnah ausgleichen können, kann es durchaus sinnvoll sein, diesen durch einen günstigen Kredit abzulösen. Der Grund: Kredite wie z.B. ein günstiger Onlinekredit bieten weitaus attraktivere Zinsen als ein Dispo und man hat aufgrund monatlich gleichbleibender Raten einen überschaubaren Plan für die Rückzahlung, ohne dass durch den Zinseszins die zu zahlende Schuldsumme weiter steigt.

Wie man den Effekt des Zinseszins berechnet

Der Effekt des Zinseszins kann einfach berechnet werden. Nehmen wir zum Beispiel an, dass Sie 1.000 Euro in ein Sparkonto mit einem Zinssatz von 5% pro Jahr einzahlen und das Kapital 10 Jahre lang unberührt lassen.

Am Ende des ersten Jahres erhalten Sie 50 Euro Zinsen (5% von 1.000 Euro). Am Ende des zweiten Jahres erhalten Sie jedoch nicht nur Zinsen auf den ursprünglichen Betrag von 1.000 Euro, sondern auch auf die 50 Euro Zinsen, die Sie im ersten Jahr verdient haben. Das bedeutet, dass Sie am Ende des zweiten Jahres 52,50 Euro an Zinsen erhalten (5% von 1.050 Euro).

Im dritten Jahr erhalten Sie Zinsen auf den Gesamtbetrag von 1.102,50 Euro und so weiter. Nach 10 Jahren hätten Sie durch den Effekt des Zinseszins ein Gesamtkapital von 1.628,89 Euro angespart.

Die Formel zur Berechnung des Effekts des Zinseszins lautet:

Endkapital = Anfangskapital x (1 + Zinssatz)n

wobei „n“ die Anzahl der Jahre ist, für die Sie das Kapital angelegt haben.

Zusammenfassung

Der Zinseszins ist ein wichtiger Faktor in vielen Finanzprodukten und Investitionsstrategien. Durch die Nutzung des Effekts des Zinseszins können Sie im Laufe der Zeit erhebliche Kapitalgewinne erzielen. Es ist jedoch auch wichtig, den Effekt des Zinseszins bei Schulden zu berücksichtigen, um ein exponentielles Wachstum der Schulden zu vermeiden. Die Berechnung des Effekts des Zinseszins ist einfach und kann Ihnen dabei helfen, fundierte Entscheidungen in Bezug auf Ihre Investitionen und Schulden zu treffen.

RTP und Volatilität: Kann man mit Mathe das Casino knacken?

Es gibt Mathegenies, die ohne Probleme jede Aufgabe lösen. Aber sind sie auch in der Lage, im Casino ihre Künste einzusetzen? Beliebte Automaten wie Eye of Horus können Spieler stundenlang in Atem halten und fesseln. Wie schön wäre es, wenn die Gewinnwahrscheinlichkeit durch mathematische Formeln beeinflusst werden könnte. Geht das? Klares Nein, denn am Ende gewinnt immer das Haus. Dennoch lässt sich zumindest die Wahrscheinlichkeit auf einen Gewinn anhand von Kennzahlen ermitteln.

Mathematik am Slot – kann damit ein Erfolg erzielt werden?

Irgendwann in der Schule stand das Thema Wahrscheinlichkeitsrechnung auf dem Lehrplan. Es ist das wichtigste Thema, wenn es um die Berechnung der Gewinnchancen im Spielcasino geht. Um zu verstehen, wie Gewinne und Verluste überhaupt berechnet werden, müssen zwei Begriffe unter die Lupe genommen werden: Volatilität und RTP.

Volatilität im Casino:

Diesen Begriff kennen wir eigentlich aus der Finanzwelt. Er beschäftigt sich mit finanziellen Schwankungen, die bei Aktienkursen, Preisen im Supermarkt und Zinssätzen zu beobachten sind. Die Volatilität dient dazu, das Risiko abzuschätzen. Auch auf Spielautomaten kann dieses Maß übertragen werden. Kann ein Spieler an einem Slot das 50.000-fache seines Einsatzes gewinnen, tritt das Ereignis mit einer sehr geringen Wahrscheinlichkeit ein. Hier wird von einer hohen Volatilität gesprochen. Es ist bedeutend realistischer und annehmbarer, dass der Einsatz verloren geht.

Die drei Stufen der Volatilität:

Slots mit niedriger Volatilität: Sie schütten häufig Gewinne aus, die allerdings nur sehr gering ausfallen. Gut geeignet sind solche Slots für ängstliche Spieler. Jackpots, Bonusfunktionen oder Freispiele sind an diesem Slot eine Seltenheit.
Mittlere Volatilität: Größere Gewinne sind möglich, allerdings gibt es dafür lange Phasen ohne Gewinne. Mit der potenziellen Höhe der Gewinne sinkt die Wahrscheinlichkeit, sie auszulösen.
Hohe Volatilität: Die Gewinne sind extrem hoch, allerdings auch extrem selten. Die Verlustwahrscheinlichkeit ist bedeutend höher, wenn es dann aber zum Gewinn kommt, ist die Summe hoch.

RTP im Casino:

Die weitere wichtige Kennzahl ist der RTP (Return to Player). Er gibt an, welcher Anteil an Einsätzen zurück an den Spieler fließt. Wenn ein Slot einen RTP von 95 % hat, werden rund 95 % der Einsätze wieder an die Spieler ausgeschüttet. Hierbei muss beachtet werden: Nicht jeder Spieler erhält 95 % seiner Einsätze wieder zurück. Stattdessen gilt der RTP übergreifend für alle Spieler.

Kartenzählen beim Blackjack – funktioniert das?

Es gibt diese beeindruckenden Geschichten von Blackjack-Spielern, die mit Kartenzählen das Casino um Hunderttausende Dollar erleichtert haben. Dabei kommt es rein auf das mathematische Verständnis an. Anhand der bereits gespielten Karten wird im Kopf die Wahrscheinlichkeit berechnet, was als Nächstes fällt. Also doch eine sichere Methode, um immer zu gewinnen? Nicht wirklich, denn Kartenzählen ist im Casino streng verboten. Online, wo es niemand überwachen könnte, ist es nicht möglich. Der Glücksspielstaatsvertrag regelt, dass Tischspiele wie Blackjack online nicht angeboten werden dürfen.

Auch beim Roulette gibt es keine Chance, das Haus durch Mathematik zu überbieten. Auch wenn es häufig angenommen wird, ist die Wahrscheinlichkeit für „Schwarz oder Rot“ nicht 50 %. Beim französischen Roulette gibt es die Null, beim amerikanischen Roulette sogar die Doppelnull. Dadurch wird die Gewinnwahrscheinlichkeit reduziert, das Haus gewinnt am Ende immer.

Fazit: Gewinne sind möglich, aber nicht berechenbar

Werfen wir einen Blick auf das wohl größte Glücksspiel der Welt: Lotto! Es ist ein Spiel mit einer hohen Volatilität. Die Wahrscheinlichkeit, hier den Jackpot zu knacken, ist äußerst gering. Dennoch gibt es immer wieder Zeitungsartikel darüber, dass 40 Millionen Euro und mehr ausgeschüttet wurden. Fair ist das Spiel, denn Gewinner gibt es. Am Ende gewinnt aber trotzdem die Lotteriegesellschaft, denn die Anzahl der Spieler steigt stetig. Glücksspiel ist und bleibt eine reine Glückssache und kann selbst von mathematischen Genies nicht geknackt werden.

So funktioniert CBD gegen Lernstress

CBD ist eine von der Cannabispflanze produzierte Verbindung, die in den letzten Jahren nicht zuletzt wegen ihres Potenzials bei der Behandlung einer Reihe von Gesundheitsproblemen und für das allgemeine Wohlbefinden Anerkennung gefunden hat.

So wurde festgestellt, dass dieses Cannabinoid Ängste und Stress reduziert, den Schlaf verbessert und sogar die Häufigkeit und Schwere von Anfällen bei behandlungsresistenter Epilepsie verringert. All diese potenziellen Vorteile werfen die Frage auf: Wirkt CBD als Nootropikum?

Was sind Nootropika?

Es wurden bereits viele Studien durchgeführt, um das medizinische und gesundheitliche Potenzial von CBD zu bewerten. Dabei gibt es immer mehr Hinweise darauf, dass das Cannabinoid starke nootropische Vorteile haben könnte. Zunächst werden Nootropika als eine Kategorie von Nahrungsergänzungsmitteln und Medikamenten definiert, die das Gehirn auf eine der folgenden Arten unterstützen können:

Bietet Schutz vor Toxinen und chemischen Ungleichgewichten
Steigert Ihre natürliche kognitive Funktion
Verbessert das Gedächtnis und das Lernen
Hilft dem Gehirn, unter stressigen Umständen zu funktionieren.

Was ist CBD?

CBD (Cannabidiol) ist eines von mindestens 100 Cannabinoiden, die in Cannabis vorkommen. Es wird häufig aus Hanf gewonnen und als Nahrungsergänzungsmittel in Form von Öl verkauft.

CBD sollte nicht mit Hanföl verwechselt werden. CBD-Öl wird aus den Blättern, Blüten und Stängeln gewonnen, während Hanföl aus den Samen der Pflanze extrahiert wird. Außerdem hat CBD nicht die psychoaktiven Wirkungen von THC. Im Gegensatz dazu kann CBD einigen dieser Wirkungen entgegenwirken – wie zum Beispiel Angstzuständen und Paranoia.

Cannabidiol Öl kaufen ist heute sehr einfach und Sie können eine Vielzahl von Produkten auf dem Markt finden. Diese Verbindung wird mit vielen der gesundheitlichen Vorteile von Cannabis in Verbindung gebracht, darunter Neuroprotektion, Schmerzlinderung, Verringerung von Angst und Depression, Linderung von krebsbedingten Symptomen und Herzgesundheit, um nur einige zu nennen.

Wie kann CBD dem Gehirn helfen?

Das Endocannabinoid-System ist Teil unseres Gehirns und wird durch zwei Cannabinoide reguliert, die natürlich im Körper vorkommen: Anandamid (AEA) und 2-Aquidonoilglycerol (2-AG). Zusammengefasst sind diese beiden Verbindungen Teil des Endocannabinoidsystems (ECS) und haben eine ähnliche Struktur wie CBD.

Daher ist bekannt, dass das ECS-System bei den folgenden Aspekten hilft:

Schlaf
Laune
Gedächtnis
Appetit und Verdauung
Temperatur
Motorische Kontrolle
Reaktion auf Schmerz und Vergnügen
Immunfunktion
Entzündung

Cannabinoidrezeptoren interagieren mit dem Nerven-, Immun- und Verdauungssystem und regulieren diese Funktionen. Daher kann CBD auch diese physiologischen Aktivitäten beeinflussen, indem es an Cannabinoidrezeptoren bindet.

Darüber hinaus hemmt CBD den Abbau von Anandamid, dem natürlich vorkommenden Cannabinoid im Körper, das mit einer beruhigenden Wirkung in Verbindung gebracht wird. Die Erhöhung der Verfügbarkeit von Anandamid kann helfen, Angstzustände zu verhindern.

Die nootropischen Vorteile von CBD

Neuroprotektion

Eine der am meisten übersehenen nootropischen Wirkungen von CBD ist, dass es die Neuronen schützen kann. Verbindungen, die als neuroprotektiv gelten, können den altersbedingten Abbau der kognitiven Funktionen verhindern oder verlangsamen und helfen, neurodegenerative Erkrankungen zu bekämpfen.

Es gibt nicht viele klinische Beweise für den neuroprotektiven Nutzen von CBD, aber Tierstudien haben es mit antioxidativen Fähigkeiten in Verbindung gebracht. Außerdem regt es die Produktion von BDNF (EN: Brain-Derived Neurotrophic Factor – DE: Vom Gehirn stammender neurotropher Faktor) an, was die Neurogenese und die Reparatur geschädigter Neuronen unterstützt.

Ängste

Die häufigste Verwendung von CBD ist die Linderung von Angstzuständen. Neben Tausenden von Rückmeldungen von regelmäßigen Anwendern wurde es in mehreren Studien mit der Linderung von Angstzuständen in Verbindung gebracht.

CBD hilft nachweislich bei verschiedenen Arten von Angstzuständen, einschließlich THC-induzierter und sozialer Ängste. Experten sind sich einig, dass diese Wirkung auf Veränderungen des Blutflusses in wichtigen Hirnregionen zurückzuführen ist. Die Aktivitäten im linken parahippocampalen Gyrus werden erhöht, während die Aktivitäten in der linken Hippocampus-Amygdala verringert werden.

Stress und Depression

Stress kann zu Depressionen führen und andersherum. Es wird angenommen, dass die positive Wirkung von CBD auf Stress und Depressionen auf seine Interaktion mit den Serotoninrezeptoren im Gehirn zurückzuführen ist.

Ein niedriger Serotoninspiegel wird mit depressiver Stimmung, Aggression, Angst, Reizbarkeit, impulsivem Verhalten und geringem Selbstwertgefühl in Verbindung gebracht. All diese Faktoren können also auch zu Stress und Depressionen führen. Vorläufige Beweise deuten darauf hin, dass CBD dazu beitragen kann, diese Symptome zu reduzieren, indem es den Serotoninspiegel in unserem Körper erhöht.

Schlafstörungen

Ein Mangel an ausreichendem Schlaf hat einen großen Einfluss auf die kognitive Leistungsfähigkeit während des Tages. Daher ist der Schlaf wohl der wichtigste Faktor für eine optimale Gehirnleistung. CBD kann bei Depressionen, Stress und Angstzuständen helfen, die häufige Ursachen für Schlaflosigkeit und schlafbezogene Probleme sind.

Sucht

Darüber hinaus hat sich CBD auch bei der Behandlung von Drogensucht als sehr vielversprechend erwiesen. Die Forschung hat es mit einem Rückgang der Abhängigkeit von Kokain, Cannabis, Tabak, Psychostimulanzien und Alkohol in Verbindung gebracht. CBD hilft bei der Sucht, indem es auf die mit einem Rückfall verbundenen Risikozustände wie Angst, Stress und Depression abzielt. Außerdem wird vermutet, dass CBD die Schaltkreise im Gehirn beeinflusst, die für das Verlangen nach Drogen verantwortlich sind.

CBD-Empfehlungen für Erwachsene

CBD ist in einer Dosis von 20 mg pro Tag und in einer Höchstdosis von 200 mg pro Tag für bis zu 30 Tage sicher und verträglich.
Die Produkte müssen auf dem Etikett Informationen über Wechselwirkungen von CBD mit Alkohol und anderen Medikamenten sowie Warnungen vor der Einnahme durch schwangere oder stillende Personen enthalten.
Die Verpackung sollte klare Dosierungsanweisungen und mögliche Nebenwirkungen enthalten, wobei zu betonen ist, dass sie sich bei höheren Dosen verschlimmern.
CBD macht nicht süchtig, aber die Aufsichtsbehörden empfehlen, in den Warnhinweisen klarzustellen, dass das Produkt nicht dazu gedacht ist, den Alkohol- und Opioidkonsum zu reduzieren.
Die Etiketten sollten Hinweise darauf enthalten, wie Verbraucher unerwünschte Wirkungen melden können, und sie sollten auch dazu ermutigt werden, mit einem Apotheker über Wechselwirkungen von Medikamenten zu sprechen.

In Empfehlungen an die Vereinten Nationen stellt die Weltgesundheitsorganisation fest, dass CBD eines der natürlich vorkommenden Cannabinoide in Cannabispflanzen ist und dass es keine Berichte über Missbrauch oder Abhängigkeit in Verbindung mit dem Konsum von reinem CBD gibt.

Fazit

Alles deutet darauf hin, dass CBD eine starke nootropische Wirkung hat, auch wenn noch viel geforscht wird, um sein volles Potenzial zu entdecken. Alles in allem ist es eine sichere und natürliche nootropische Option und eine großartige Ergänzung für jedes Wellness-Programm.

Zinsrechnung so geht’s!

Die Zinsrechnung ist eines der nützlichsten mathematischen Themen, die man in der Schule lernt. Die Fläche einer Kurve zu berechnen ist nicht ganz so alltagstauglich, wie die Raten eines Kredites zu berechnen. Vor allem wenn man sich für Investments interessiert und rüber Dogecoin kaufen nachdenkt. Dabei kann die Zinsrechnung helfen zu berechnen, um wie viel das eigene Investment wächst bzw. schrumpft, je nachdem, wie sich der Dogecoin Kurs bewegt.

Die Grundlage: Prozentrechnung

Die Zinsrechnung basiert in erster Linie auf der Prozentrechnung. Deshalb hier eine kurze Wiederholung der Grundlagen dieser. Die drei wichtigen Begriffe und Zeichen sind natürlich:

Grundwert: G
Prozentwert: W
Prozentsatz: p %

Die Formel um den Prozentsatz (p steht für die Nummer vor dem % Zeichen) zu berechnen geht wie folgt:

W/G = p %

Je nachdem welche Zahl du suchst, musst die Formel natürlich entsprechend umstellen.

Zinsberechnung: Begriffe und Formeln

Bei der Zinsberechnung geht es, wie der Name dir schon verrät, um die Berechnung der Zinsen für das Guthaben auf einem Sparkonto. Wenn du dir Geld von der Bank leihst, sind auch die Zinsen wichtig, die du an die Bank zahlen musst.

Deine Berechnung der Zinsen ist die gleiche wie die Prozentrechnung. Da das Rechnen mit Geld aus dem Finanzbereich kommt, werden hier andere Begriffe verwendet. Diese sind wie folgt:

Aus dem Grundwert (G) wird in der Zinsrechnung das Kapital (K), welches sowohl für Guthaben, aber auch für Kredit verwendet wird.

Prozentwert wird in der Zinsrechnung als Zinsen (Z) bezeichnet.

Der Prozentsatz wird in der Zinsrechnung zum Zinssatz, der aber immer noch mit einem p % dargestellt wird. Die Zinsen werden in der Regel „pro Jahr“ berechnet, welches durch ein „p. a.“ hinter p % angedeutet wird. „p. a.“ steht für „per annum“.

Die Zinsen, welche du innerhalb eines Jahres erhalten wirst, kannst du dann wie Folgenden berechnen. Nicht erschrecken in dieser Formel werden nicht p % verwenden, sondern p und dann durch den Faktor 100 teilen, das Ergebnis ist aber dasselbe.

Z = (K x p) / 100

Beispiele für die Zinsrechnung

Die Theorie ist natürlich immer wichtig, aber um die Zinsrechnung wirklich zu verstehen, braucht es in erster Linie Beispiele, an denen man erkennen, wie die Formel verwendet wird.

Berechnung von Zinsen

Lisa legt ein Kapital K = 700 € an. Der Zinssatz beträgt p % = 0,03 = 3 % p.a., das bedeutet: p = 3. Die Zinsen für ein ganzes Jahr kann man nun mit der Formel zur Zinsrechnung berechnen.

Zinsen für das Jahr:

Z = (K x p) / 100

Z = (700 x 3) / 100

Z = 2100 / 100

Z = 21

Mit dieser kurzen Rechnung hast du herausgefunden, dass Lisas Kapital nach einem Jahr Zinsen von 21 € erhält. Doch das ist nicht alles, was du mit dieser Formel berechnen kannst, auch Zinsen pro Monat oder Tag sind möglich. So sehen die Formeln dafür aus:

Zinsen pro Monat oder Tag

Die Berechnung hierfür ist ganz einfach. Wenn du pro Monat suchst, dann teilst du die Jahreszinsen einfach durch 12 solltest du pro Tag suchen, dann durch 360, da ein Bankjahr nur 360 Tage hat.

Z = ((K x p) / 100) / 12

Z = ((700 x 3) / 100) / 12

Z = (2100 / 100) / 12

Z = 21 / 12

Z = 1,75

Wenn du nach K oder p suchst, musst die Formeln natürlich entsprechend umstellen.

Zins und Zinseszins

Lisa verdient Z = 21 € mit einem p % = 0,03 und einem K = 700 €. Diese Zinsen werden dem Kapital hinzugerechnet. Das bedeutet, dass Lisa nach einem Jahr bereits 700 € + 21 € = 721 € hat. Sie kann das Geld wieder mit p % = 0,03 (also p = 3) anlegen. So entwickelte sich das Kapital wie folgend:

Z = (721 x 3) / 100 = 21,63

Im Zweiten Jahr erhält sich also 0,63 € mehr in Zinsen, da das Ausgangskapital um 21 € gewachsen ist. Diesen Effekt nennt man Zinseszins. In der Regel wird diese Formel dafür verwendet:

N steht hier für die Zahl der Jahre. In unserem Beispiel würdest du also für n = 2 eintragen. Dadurch erhältst du die folgende Rechnung:

Mit diesen Formeln solltest du einen guten Überblick über die wichtigsten Rechnungen in der Zinsrechnung erhalten.

Zinsrechnung

Zinsrechnung ist angewandte Prozentrechnung. Wir benötigen die Zinsrechnung überall, wo wir mit Zinsen rechnen – insbesondere, wenn wir die Kosten für einen Kredit oder den Gewinn aus einer Geldanlage berechnen wollen. In diesem Artikel erfährst du anhand von Beispielen und Erklärungen zur Zinsrechnung, wie du praktisch mit Zinsen rechnest. Wenn du dich noch nicht so gut mit der Prozentrechnung auskennst, lies dir zuerst die Seiten zur Prozentrechnung und zum Dreisatz durch. Dort lernst du Begriffe wie Prozentsatz, Grundwert und Prozentwert kennen, die du für die Zinsrechnung benötigst.

Übersicht über die wichtigsten Formeln der Zinsrechnung

Hier findest du eine knappe Übersicht über die wichtigsten Formeln der Zinsrechnung. Weiter unten auf der Seite stehen die detailierten Erklärungen zu den Formeln.

Formel	Bedeutung
	Jahreszins
	Tageszins (Deutsche Methode)
	Monatszins (Deutsche Methode)
	Endkapital nach einer Zinsperiode
	Endkapital mit Zinseszinsen
	Sparkassenformel

Grundbegriffe der Zinsrechnung

Zinssatz: Der Zinssatz wird als Prozentsatz angegeben und beschreibt, wie viele Zinsen abhängig vom Kapital für einen bestimmten Zeitraum (die Zinsperiode) gezahlt werden. In den Formeln geben wir den Zinssatz als p an.
Kapital: Als Kapital bezeichnen wir die angelegte Geldmenge, für die Zinsen gezahlt werden. Zahlt man beispielsweise 100 Euro auf ein Sparkonto ein, sind diese 100 Euro das Anfangskapital. Wenn wir nicht mit einer Geldanlage, sondern mit einem Kredit rechnen, ist die geliehene Geldsumme das Kapital. In den Formeln geben wir das Kapital als K und das Endkaptial als Z an.
Zinsperiode: Zinsen werden immer für einen bestimmten Zeitraum bezahlt. Die Zeit, für die ein Zinssatz angegeben wird, nennt man Zinsperiode. In der Zinsrechnung betrachtet man üblicherweise einen Jahreszins. Weiter unten zeigen wir, wie man rechnen muss, wenn man einen anderen Zeitraum als die Zinsperiode betrachtet.

Zu dem Begriff „Zinssatz“ noch eine wichtige Anmerkung: Außer „Zinssatz“ hört man in der Zinsrechnung manchmal den Begriff „Zinsfuß“. Dabei bezeichnet der Zinsfuß die Zahl vor dem Prozentzeichen und der Zinssatz entspricht dem Prozentsatz. Falls wir also einen Zinssatz von 2,5 % = 0,025 haben, ist der Zinsfuß 2,5.

Jahreszins: Zinsen für ein Jahr berechnen

Im einfachsten Fall ermittelt man mit der Zinsrechnung, wie viele Zinsen man für sein Anfangskapital in einer Zinsperiode erhält oder wie viele Zinsen man für einen Kredit in einer Zinsperiode zahlt. Da die Zinsperiode in der Zinsrechnung üblicherweise ein Jahr beträgt, berechnet man also den Jahreszins.

Die Zinsen errechnen sich aus dem Produkt aus Zinssatz (p) und Anfangskapital (K). Die Formel lautet:

Formel für den Jahreszins

Auf die Prozentrechnung übertragen, entspricht der Jahreszins dem Prozentwert des Zinses (Prozentsatz) bezogen auf das Kapital (Grundwert).

Möchte man wissen, wie sich der Wert des angesparten Gelds nach einem Jahr entwickelt hat, addiert man zum Jahreszins den ursprünglichen Kapitalwert und erhält das sogenannte Endkapital. Alternativ addiert man zum Zinssatz einhundert Prozent. Die Formel für das Endkapital lautet daher:

Formel für das Endkapital nach einer Zinsperiode

Beispiel: Angenommen wir legen 400 Euro zu einem Zinssatz von 2,25 % für ein Jahr an. Wir erhalten nach einem Jahr folgende Zinsen ausgezahlt:

Beispiel für die Berechnung des Jahreszins

Der Wert des Endkapitals beträgt:

Beispiel für die Berechnung des Endkapitals nach einer Zinsperiode

Zinsen für einzelne Monate oder Tage berechnen

Manchmal möchte man Zinsen nicht für ein ganzes Jahr, sondern für einen kürzeren Zeitraum berechnen. Die Zinsrechnung bietet verschiedene Möglichkeiten, den Zinssatz auf einzelne Tage herunterzurechnen. Die sogenannten „Deutschen Methode“ rechnet für das ganze Jahr mit 360 Tagen und für jeden Monat mit 30 Zinstagen. Sie unterscheidet sich von der tagegenauen Methoden, die mit der tatsächlichen Anzahl von Tagen pro Jahr (365, beziehungsweise 366 in Schaltjahren) und pro Monat rechnet. Wir stellen hier die „Deutsche Methode“ der Zinsrechnung genauer vor.

Zur Berechnung der Tageszinsen nutzt man in der Zinsrechnung den einfachen Dreisatz. Berechnet man mit der „Deutschen Methode“, teilt man den Zinssatz durch 360, um den Zinssatz pro Tag zu erhalten. Diese Tageszinsen multipliziert man mit der Anzahl der Tage. So berechnet man die Zinsen für mehrere Zinstage (t) so:

Formel zur Berechnung von Tageszinsen

Werden also 200 Euro für 24 Tage zu einem Zinssatz von 4 Prozent verzinst, erhält man Zinsen in Höhe von:

Beispiel für die Berechnung von Tageszinsen

Auch andere Zinsperioden werden in der Zinsrechnung auf diese Weise berechnet. Die Gleichung zur Berechnung der Monatszinsen lautet beispielsweise:

Formel zur Berechnung von Monatszinsen

Zinseszins

Wenn man Geld über einen längeren Zeitraum anlegt und die Zinsen nicht abhebt, sondern ebenfalls anspart, erhält man in den folgenden Jahren nicht nur auf den ursprünglich eingezahlten Betrag Zinsen, sondern auch auf die früheren Zinsen. Zinsen, die auf Zinsen gezahlt werden, bezeichnet man in der Zinsrechnung als Zinseszins.

Die folgende Tabelle zeigt an einem Beispiel der Zinseszinsrechnung, wie Zinseszinsen den gesparten Betrag erhöhen. In diesem Beispiel wird ein Kapital von 300 Euro auf ein Sparkonto mit vierprozentiger Verzinsung eingezahlt. Die mittlere Spalte zeigt den Wert des Kapitals mit und die recht Spalte den Wert ohne Zinseszins

Jahr	Mit Zinseszins	Ohne Zinseszins
1	300 Euro	300 Euro
2	312 Euro	312 Euro
3	324,48 Euro	324 Euro
4	337,46 Euro	336 Euro
5	350,96 Euro	348 Euro
6	365 Euro	360 Euro
7	379,60 Euro	372 Euro
8	394,78 Euro	384 Euro
9	410,57 Euro	396 Euro
10	426,99 Euro	408 Euro
…
50	2.050 Euro	888 Euro

Der Zinseszins hat in diesem Beispiel das Kapital über fünfzig Jahre beinahe versiebenfacht. Bei einfacher Verzinsung ist das Endkapital lediglich knapp dreimal so groß wie der Geldbetrag, den man angelegt hat.

In der Zinseszinsrechnung steigt der Wert des Kapitals exponentiell. Die folgende Grafik zeigt wie sich der Wert des angelegten Geldes aus dem obigen Beispiel mit der Zeit entwickelt. Die grüne Line zeigt was das Kapital bei einfacher Verzinsung nach einer bestimmen Zahl an Jahren Wert ist, die rote Line zeigt die Entwicklung des Kapitals mit Zinseszinsen:

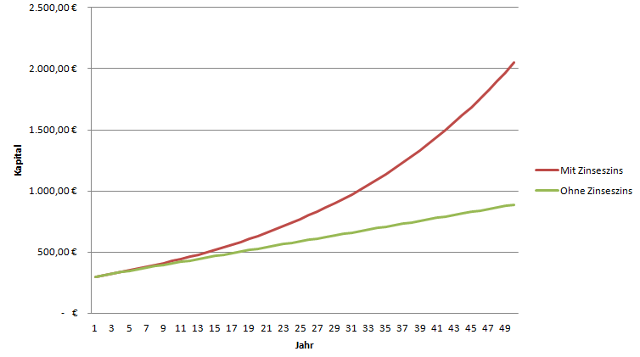
Diagramm zur Zinseszinsrechnung

Um die Verzinsung mit Zinseszins zu berechnen, nutzt man folgende Formel:

Formel zur Berechnung der Kapitalentwicklung mit Zinseszinsen

In dieser Formel steht K für das Anfangskapital, Z für das Endkapital, p für den Zinssatz und t für die Anzahl der Zinsperioden.

Zinsen bei jährlicher Einzahlung mit Zinseszinsrechnung

Bei längerfristigen Sparplänen ist es üblich, nicht nur einen anfänglichen Geldbetrag anzulegen, sondern zusätzlich jährlich einen festgelegten Betrag einzuzahlen. Diesen Betrag bezeichnet man in der Zinsrechnung als Annuität. In allen Folgejahren wird er ebenfalls verzinst.

Der Wert des Endkapitals wird mit der sogenannten Sparkassenformel berechnet:

Sparkassenformel mit Herleitung

In der Sparkassenformel steht wie in der Zinsrechnung üblich K für das Anfangskapital, K_n für die Annuität, Z für das Endkapital und q für 1 + p.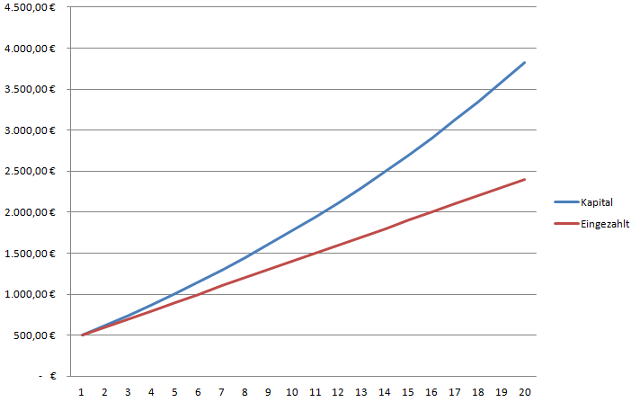 Kapitalentwicklung bei jährlicher Einzahlung (Diagramm zur Sparkassenformel)

Diese Grafik, zeigt die Kapitalentwicklung, bei einmaliger Einzahlung von 500 Euro und einer jährlichen Einzahlung von 100 Euro bei 4 Prozent Zinsen. Nach 20 Jahren wurde ein Betrag von 2.400 Euro eingezahlt, der mit Verzinsung auf 3.820,55 Euro angewachsen ist.

Zinssätze berechnen

In den bisherigen Formeln der Zinsrechnung waren Zinssatz, Kapital und die Zinsperioden gegeben. Manchmal kennt man jedoch statt des Zinssatzes nur das Endkapital. Die Frage, die man damit beantwortet, lautet beispielsweise: „Zu welchem Zinssatz muss ich 100 Euro anlegen, damit daraus nach zehn Jahren 400 Euro werden?“.

Die Formel zur Berechnung des Zinssatzes mit dem Endkapital Z und dem angelegten Betrag K lautet bei einer Zinsperiode von einem Jahr:

Formel zur Berechnung des Zinssatzes nach einer Zinsperiode

Und bei mehrjähriger Verzinsung:

Formel zur Berechnung des Zinssatzes bei mehreren Zinsperioden

Die oben gestellte Frage beantwortet die Zinseszinsrechnung mit:

Beispiel zur Berechnung von Zinssätzen

Man muss das Kapital also über zehn Jahre mit knapp fünfzehnprozentiger Verzinsung anlegen, um auf das angestrebte Endkapital zu kommen.

Vollständige Induktion

Die vollständige Induktion ist ein Beweisverfahren, das beim Beweisen von Aussagen im Zahlenraum der natürlichen Zahlen eine wichtige Rolle spielt. Beweise per vollständiger Induktion werden immer in zwei Schritten vollzogen: Zum einen wird bewiesen, dass eine Aussage für eine kleine natürliche Zahl n₀ gilt (üblicherweise ist n₀ = 1). Zum andern wird gezeigt, dass die Aussage falls sie für ein beliebiges n gilt auch für n + 1 gilt. Daraus kann geschlossen werden, dass sie für jedes n > n₀ gilt.

In der vollständigen Induktion beweisen wir also, dass eine Aussage für 1 gilt und dass sie, falls sie für eine Zahl gilt, auch für ihren Nachfolger gilt. Weil die Aussage für 1 gilt, gilt sie also auch für 2. Weil sie für 2 gilt, gilt sie auch für 3. Weil sie für 3 gilt, auch für 4… Da wir theoretisch in dieser Weise immer weiter machen können, schließen wir, dass die Aussage für jede natürliche Zahl gilt, egal wie groß sie auch sein mag.

Bildhaft kann man sich die vollständige Induktion wie eine Reihe von Dominosteinen vorstellen, die alle nacheinander umfallen: Wir schubsen den ersten Stein um (die Behauptung: „Der erste Stein fällt um“, ist damit wahr). Wir wissen, wenn ein Stein umfällt, stößt er auch seinen Nachbarn um (wenn die Annahme: „Der n-te Stein fällt um“, stimmt, folgt: „Der „n + 1“-te Stein fällt um“). Daraus können wir schließen, dass irgendwann jeder einzelne Dominostein umfällt.

Induktionsbeginn, Induktionsannahme und Induktionsschritt

Die Begriffe Induktionsbeginn, Induktionsannahme und Induktionsschritt bezeichnen die einzelnen Teile eines Beweises per vollständiger Induktion. Wenn wir einen Beweis per vollständiger Induktion ausführen, darf keiner dieser Teile fehlen:

Als Induktionsbeginn bezeichnen wir den Beweis der Behauptung für n₀. Dieser Beweis muss direkt geführt werden, beispielsweise, indem wir n₀ = 1 in den Term einfügen, über den wir eine Aussage machen möchten.
Die Induktionsannahme ist die Annahme, dass unsere Behauptung für ein beliebiges n gilt. Die Annahme wurde von uns noch nicht bewiesen. Für den Induktionsschritt nehmen wir sie als wahr an.
Mit dem Induktionsschritt zeigen wir, dass unsere Behauptung für n + 1 gilt, falls sie für n gilt.

Beispiel für die vollständige Induktion

Die vollständige Induktion wird gerne genutzt um Aussagen über Reihen und Folgen zu beweisen. Als Beispiel wollen wir folgende Aussage beweisen:

Die Summe aller ungeraden Zahlen kleiner 2*n ist gleich n zum Quadrat

In Worten: „Die Summe aller ungeraden Zahlen kleiner 2*n ist gleich n zum Quadrat“. Diese Aussage stimmt beispielsweise für alle ungeraden Zahlen kleiner 8 (n=4 und n²=16):

Die Summe aller ungeraden Zahlen kleiner 8 ist gleich 4 zum Quadrat also 16

Für den Induktionsbeginn zeigen wir zunächst, dass die Aussage für n₀ = 1 gilt. Dies ist trivial:

Induktionsbeginn

Jetzt nehmen wir an, dass unsere Behauptung für ein beliebiges n gilt. Dies ist unsere Induktionsannahme. Unter dieser Annahme versuchen wir zu zeigen, dass sie auch für n + 1 gilt (Induktionsschritt):

Induktionsschritt

Der Induktionsschritt ist also korrekt und die Behauptung gilt für alle n > 1, d.h. für alle natürlichen Zahlen. Um die Richtigkeit des Induktionsschritt zu zeigen, haben wir in der Umformung des blau markierten Terms die Induktionsannahme genutzt.

Zusammenhang von Induktionsannahme und Induktionsbeginn

Erfahrungsgemäß bereitet es Schülern manchmal Probleme, das Verhältnis von Induktionsannahme und Induktionsbeginn in der volltständigen Induktions richtig zu begreifen. Wir wollen es deshalb noch einmal im Detail betrachten. Zunächst eine wichtige Unterscheidung:

Beim Induktionsbeginn zeigen wir für ein konkretes n₀, dass die Aussage war ist. Üblicherweise ist n₀ = 1.
Bei der Induktionsannahme nehmen wir an, dass die Aussage, die wir beweisen wollen, für ein irgendein beliebiges n wahr ist. Ob sie tatsächlich war ist, wissen wir nicht. Ebensowenig treffen wir eine Aussage, um welche Zahl es sich bei n handelt und ob die Aussage auch für andere n gilt.

Der Induktionsbeginn ist wie im oberen Beispiel häufig trivial, weil wir für ihn einfach nur 1 in die zu beweisende Aussage einsetzen müssen. Trotzdem dürfen wir ihn nicht vernachlässigen. Fehlt er, ist auch der Induktionsschritt wertlos.

Der Induktionsschritt ist selbst dann korrekt, wenn wir mit ihm aus einer falschen Aussage auf eine andere falsche Aussage schließen. Wir könnten beispielsweise annehmen, dass für ein beliebiges n gilt, dass 2n + 5 eine gerade Zahl ist. Dann schließen wir im Induktionsschritt, dass dies auch für n + 1 gilt, weil eine gerade Zahl zu der wir 2 addieren wieder gerade ist. Damit können wir aber noch lange nicht beweisen, dass 2n + 5 für jede natürliche Zahl n gerade ist. Wir finden nämlich keine einzige konkrete Zahl n₀ für die diese Aussage wahr ist.

Obwohl der Induktionsschritt korrekt ist, lässt sich diese Aussage also nicht per vollständiger Induktion beweisen, weil der Induktionsbeginn nicht gelingt. Oder um noch einmal auf das Bild der kippenden Dominosteine zurückzukommen: Alle Steine bleiben stehen, wenn nicht wenigstens ein Stein als erstes kippt.

Summenzeichen

Das Summenzeichen (auch als „Summationszeichen“ oder „Summationssymbol“ bezeichnet) wird verwendet, wenn wir eine Summe über endlich oder unendlich viele Glieder einer Reihe bilden wollen, wobei der Wert der Glieder von einer Variablen abhängt. Eine Summe wird mit dem Summenzeichen in dieser Weise geschrieben:

Summenzeichen

Zu dem Summenzeichen gehören verschiedene Bestandteile, die oben farblich markiert sind:

Die Laufvariable, bzw. der Laufindex (blau): Dies ist die veränderliche Variable der Summe. Für jeden Wert der Laufvariable gibt es genau einen Summanden. Für die Laufvariable, bzw. den Laufindex werden üblicherweise die Buchstaben i, j, k oder l gewählt.
Der Startwert (rot): Dies ist der kleinste Wert, den die Laufvariable annimmt. Der Startwert ist eine ganze Zahl.
Der Endwert (grün): Dies ist der größte Wert, den die Laufvariable annimmt. Der Endwert ist eine ganze Zahl. Falls hier das Unendlichkeitszeichen (eine liegende Acht: ∞) steht, wird die unendliche Summe gebildet, wobei die Laufvariable den Wert des Startwerts und jeder Ganzzahl größer als dem Startwert annimmt.
Die Summanden (orange): Die Summanden bestehen üblicherweise aus einer Funktion, die von der Laufvariable abhängt.

Wenn die Summe wie oben mit Start- und Endwert geschrieben ist, nimmt die Laufvariable den Wert jeder ganzen Zahl zwischen dem Start- und dem Endwert ein (inklusive Startwert und Endwert). Für jeden ihrer Werte wird genau ein Summand addiert. Ein Beispiel für solch eine Summe ist die Summe aller Quadrate der ganzen Zahlen zwischen eins und fünf:

Beispiel für das Summenzeichen: Die Summe aller Quadrate der ganzen Zahlen von eins bis fünf

Die Laufvariable ist hier i, der Startwert 1, der Endwert 5 und die Summanden werden über die Funktion i² gebildet, wobei i alle Werte von eins bis fünf einnimmt.

Rechenregeln für das Summenzeichen

Das Summenzeichen ist eine verkürzende Schreibweise für Summen. Deshalb können wir einzelne Summanden aus dem Summenzeichen herausnehmen und einzeln notieren:

Summanden ausgehend vom Endwert aus dem Summenzeichen herausnehmen

Hier wurde im ersten Schritt der Summand a_n aus dem Summenzeichen herausgenommen und einzeln notiert. Der Endwert wurde dafür um eins veringert. Danach wurde auch der Summand a_n-1 aus dem Summenzeichen herausgenommen. Der Endwert wurde dafür noch einmal um eins verringert. Im letzten Schritt wurden alle Summanden aus dem Summenzeichen herausgenommen.

Natürlich können wir nicht nur vom Endwert ausgehen, um Summanden einzeln zu notieren, sondern auch vom Startwert. Dabei muss der Startwert entsprechend angepasst werden:

Summanden ausgehend vom Startwert aus dem Summenzeichen herausnehmen

Wir können eine Summe auch in mehrere Teilsummen aufteilen:

Summen aufteilen

So können wir auch Summanden für Laufwerte zwischen Start- und Endwert einzeln notieren:

Innere Summanden lassen sich ebenfalls einzeln schreiben

Summen über konstante Summanden

Manchmal kommt es vor, dass die einzelnen Summanden gar nicht vom Wert der Laufvariable abhängen. a_i ist dann gleich einer Konstante c. In diesen Fällen können wir die Summe einfach berechnen, indem wir den Wert der Konstante mit der Anzahl der Summanden multiplizieren. Die Anzahl der Summanden in einer Summe entspricht der Differenz zwischen Endwert und Startwert plus eins:

Summe über konstante Summanden

Das sieht beispielsweise so aus:

Beispiel für eine Summe über konstante Summanden

Assoziativgesetz

Das Assoziativgesetz besagt, dass es egal ist, in welcher Reihenfolge die Summanden einer Summe aufsummiert werden. Dies können wir uns zunutze machen, wenn die Summanden selbst wieder Summen enthalten:

Anwendung des Assoziativgesetz auf das Summenzeichen

Distributivgesetz

Das Distributivgesetz besagt, dass es egal ist, ob man zuerst jeden Summanden mit einem Faktor multipliziert und danach die Summe der Produkte bildet, oder ob man zuerst die Summanden addiert und anschließend die Summe mit dem Faktor multipliziert. Dies gilt natürlich auch für das Summenzeichen. So können wir Faktoren aus den Summanden ausklammern und vor das Summenzeichen schreiben:

Anwendung des Distributivgesetz auf das Summenzeichen

Indexverschiebung

Die Laufvariable nimmt alle Werte zwischen Startwert und Endwert ein und wird in die Summanden eingefügt. Wir können den Startwert und den Endwert jeweils um denselben Betrag erhöhen oder veringern. Wenn wir den Wert, den wir in die Summanden einsetzen, um denselben Betrag mit umgekehrten Vorzeichen anpassen, erhalten wir weiterhin dieselbe Summe. Falls wir also beispielsweise Start- und Endwert jeweils um drei erhöhen, müssen wir von der Laufvariablen drei abziehen, bevor wir sie im Summanden einsetzen:

Indexverschiebung: Allgemeines Vorgehen

Wie die Indexverschiebung funktioniert versteht man am besten, wenn man sich ein Beispiel dazu ansieht:

Beispiel für die Indexverschiebung

Die Indexverschiebung ist besonders dann praktisch, wenn wir zwei Summen addieren möchten, bei denen Startwert und Endwert um denselben Betrag voneinander abweichen:

Anwendung der Indexverschiebung

Spezielle Notationsformen

Die Art in der das Summenzeichen geschrieben wird, kann manchmal von der oben aufgeführten Form abweichen. Zwei Spezialfälle wollen wir hier betrachen: Summen über Summen und Summen über Indexmengen.

Zwei Laufvariablen: Summen über Summen

Es kommt immer mal wieder vor, das in einer Rechnung Summen über Summen gebildet werden, so dass zwei Summenzeichen direkt hintereinander stehen. Diese Summenzeichen lassen sich zusammenfassen, indem man beide Laufvariablen an einem Summenzeichen notiert:

Zwei Laufvariablen an einem Summenzeichen

Unterhalb des Summenzeichen werden beide Laufvariablen mit ihrem jeweiligen Startwert notiert, darüber beide mit ihrem jeweiligen Endwert. Um deutlich zu machen, welcher Endwert zu welcher Laufvariable gehört, muss die jeweilige Laufvariable explizit angegeben werden.

Wenn wir also ein Summenzeichen mit zwei Laufvariablen haben, so bedeutet dies, dass sie Summe über alle Kombinationen von möglichen Werten der Laufvariablen gebildet werden:

Beispiel für zwei Laufvariablen an einem Summenzeichen

Summen über Indexmengen

Bis jetzt haben wir nur Summen betrachtet, bei denen die Indexwerte aus einer kontinuierlichen Abfolge ganzer Zahlen stammen. Manchmal möchte man jedoch über andere Mengen summieren. In diesem Fall werden die Laufvariable und die Menge unterhalb des Summationszeichens notiert. Der Endwert entfällt hierbei. Sei A eine Menge, so wird eine Summe über Indizees aus A so dargestellt:

Summe über eine Indexmenge

Die Summe der Wurzeln aus 16, 81 und 144 kann beispielsweise so notiert werden:

Beispiel für eine Summe über eine Indexmenge

Ein anderes Beispiel ist die Summe aller Teiler von 20:

Beispiel für eine Summe über eine kokmplexere Indexmenge

(Die Menge unterhalb des Summenzeichen ist folgendermaßen zu verstehen: „Alle natürlichen Zahlen n mit der Eigenschaft, dass es irgendeine natürliche Zahl m gibt, so dass n mal m gleich zwanzig ist.“)

Reihen in der Mathematik

Eine Reihe ist in der Mathematik eine Summe über die Glieder einer Folge. Die Reihe über die ersten n Glieder einer Folge (a_n) wird als s_n bezeichnet. Mathematisch werden Reihen über das Summenzeichen notiert und es gilt:

Allgemeine Definition von Reihen

Einige wichtige Reihen in der Mathematik sind:

Formel	Bedeutung
	Gaußsche Summenformel
	Arithmetische Reihe
	Geometrische Reihe
	Unendliche geometrische Reihe für -1 < q < 1

Endliche und unendliche Reihen

Wir unterscheiden zwischen endlichen und unendlichen Reihen, je nachdem, ob n endlich ist oder nicht. Der Wert einer unendlichen Reihe beträgt:

Wert einer unendlichen Reihe

Dieser Wert ist nur definiert, falls die Reihe für große Werte von n konvergiert. Das bedeutet, es muss einen Wert s geben, so dass für jeden beliebig kleinen Bereich um s ein n’ existiert mit der Eigenschaft, dass alle s_n für n > n’ innerhalb dieses Bereiches liegen.

Wichtige Reihen in der Mathematik

Arithmetische Reihe

Eine arithmetische Reihe ist die Summe über die ersten n Glieder einer arithmetischen Folge. Für jede arithmetische Folge gilt ein Bildungsgesetz in dieser Form:

Arithmetische Folge

Eine arithmetische Reihe ist somit definiert als:

Arithmetische Reihe

Für die Summe über die ersten n natürlichen Zahlen gilt die sogenannte Gaußsche Summenformel:

Gaußsche Summenformel

Somit gilt für arithmetische Reihen:

Arithmetische Reihe vollständig

Geometrische Reihe

Eine geometrische Reihe ist eine Summe über n Glieder einer geometrischen Folge. Für jede geometrischen Folge gilt ein Bildungsgesetz in dieser Form:

Geometrische Folge

Eine geometrische Reihe ist somit definiert als:

Geometrische Reihe

Falls q kleiner als 1 und größer als -1 ist, konvergiert die Geometrische Reihe. Dann gilt:

Geometrische Reihe für q < 1

Für c = 1 und q = 1/2 gilt beispielsweise:

Beispiel für die Konvergenz der geometrischen Reihe

Reihen in der Mathematik

Reihen kommen in der Mathematik relativ häufig vor. Dabei handelt es sich um eine unendliche Folge von Zahlen, die nach einem bestimmten Schema angeordnet sind. Eine Reihe kann zum Beispiel aus den natürlichen Zahlen 1, 2, 3, 4, 5,… bestehen.

Bei einer solchen Reihe wird jede Zahl um 1 erhöht. Das bedeutet, dass die nächste Zahl immer um 1 größer ist als die vorherige.
Natürlich können Reihen auch anders aussehen. So kann zum Beispiel die Reihe 2, 4, 6, 8,…bestehen. In diesem Fall wird jede Zahl um 2 erhöht. Auch hier gilt wieder: Die nächste Zahl ist immer um 2 größer als die vorherige.

Quotientenregel

Die Quotientenregel besagt, wie der Quotient zweier Funktionen abgeleitet wird. Sie lautet:

Quotientenregel

In der Kurzschreibweise wird die Quotientenregel häufig auch so notiert.

Kurzform der Quotientenregel

Beispiele für die Quotientenregel

Die Quotientenregel wird am besten an ein paar Beispielen deutlich. Als erstes wollen wir dafür diesen Bruch ableiten:

Erstes Beispiel für die Quotientenregel

Zunächst leiten wir Zähler und Nenner jeweils einzeln ab. Die Ableitung des Zählers ist:

Ableitung des Zählers

Und die Ableitung des Nenners lautet:

Ableitung des Nenners

Wenn wir die Ableitungen in die Formel für die Quotientenregel einsetzen, erhalten wird:

Anwendung der Quotientenregel

Als nächstes sehen wir uns die Ableitung für den Tangens an. Da der Tangens als Quotient aus Sinus und Cosinus gebildet wird, können wir die Quotientenregel für die Ableitung nutzen:

Ableitung des Tangens mit der Quotientenregel

Herleitung der Quotientenregel

Mit der Kehrwertregel können wir die Quotientenregel als Spezialfall der Produktregel herleiten. Dafür betrachten wir den Quotienten der beiden Funktionen als Produkt des Zählers mit dem Kehrwert des Nenners:

Quotient als Produkt des Zählers mit dem Kehrwert des Nenners

Unter Anwendung der Quotientenregel erhalten wir:

Herleitung der Quotientenregel