Die binomischen Formeln gehören zum grundlegenden Rüstzeug für Schüler aller Schularten. Mit Hilfe der binomischen Formeln wird die Potenz der Summe zweier Zahlen (häufig als a und b bezeichnet) gebildet. Die Rechnung mit Potenzen wird auf diese Weise erheblich vereinfacht. Anstatt nämlich zwei große Zahlen multiplizieren zu müssen, brauchen die Schüler nach Anwendung der binomischen Formeln nur noch zwei kleinere Zahlen miteinander zu multiplizieren und deren Summe zu bilden.
In der Mathematik werden drei binomische Formeln unterschieden:
- Die erste binomische Formel beschreibt den Fall, dass zwei Zahlen a und b addiert und die Summe potenziert wird.
- Die zweite binomische Formel wird in dem Fall angewendet, dass b von a subtrahiert wird.
- Die dritte binomische Formel wird schließlich angewendet, wenn wir zwei unterschiedliche Faktoren haben, nämlich einen, in dem a und b addiert, und einen, in dem b von a subtrahiert wird.
Zu den wichtigen Punkten, die ein Schüler im Zusammenhang mit den binomische Formeln lernen muss, gehört es zu erkennen, welche der drei binomischen Formeln in einer konkreten Aufgabe angewandt werden muss.
Binomische Formeln
| Formel | Bedeutung |
|---|---|
| Erste binomische Formel | |
| Zweite binomische Formel | |
| Dritte binomische Formel |
Grafische Herleitung
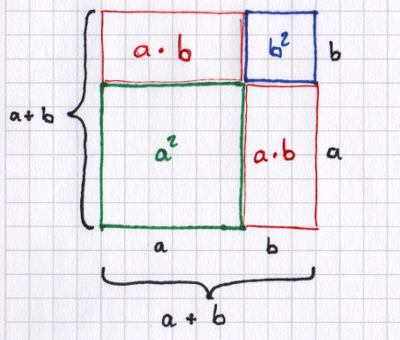
Die obige Grafik zeigt, wie sich die erste binomische Formel grafisch herleiten lässt. Sie zeigt ein Quadrat, dessen Kantenlänge a + b beträgt. Seine Fläche lässt sich daher mit (a + b)2 berechnen. Dieses Quadrat setzt sich wiederum aus verschiedenen Flächen zusammen. Die grün umrandete Fläche entspricht mit a2 dem ersten Summanden der binomischen Formel, die blau umrandete mit b2 dem letzten Summanden. Die beiden rot umrandeten Rechtecke, deren Fläche jeweils a * b beträgt, entsprechen zusammen dem mittleren Summanden 2ab. Anhand dieser einprägsamen Grafik lässt sich sofort erkennen, dass die Fläche des großen Quatdrats (a + b)2 der gemeinsamen Fläche der beiden kleinen Quadrate und der beiden Rechtecke (a2 + 2ab + b2) entspricht. Hierin finden wir also die erste binomische Formel wieder:
Herleitung der 3 binomischen Formeln
Die binomischen Formeln werden hergeleitet, in dem zuerst die Potenz hoch zwei aufgelöst wird in die Multiplikation zweier Summen (bzw. zwei Differenzen oder einer Summe mit einer Differenz). Anschließend wird zuerst die Summe in der vorderen Klammer ausmultipliziert. Jeder der beiden Summanden wird mit der zweiten Klammer multipliziert. Anschließend wird auch die zweite Klammer ausmultipliziert. Wir haben nun vier Summanden mit unterschiedlichen Vorzeichen. Zwei der Summanden sind die Quadrate von a und b. Die beiden anderen Summanden jeweils das Produkt aus a und b. Die drei binomischen Formeln unterscheiden sich in den Vorzeichen ihrer Summanden. Durch Zusammenfassung der Summanden werden die binomischen Formeln in ihre endgültige Form aus drei, bzw. zwei Summanden gebracht.
