Kategorie: Formeln

Aktuelle Diskussionen um die Nutzung von Mobiltelefonen in den Klassenzimmern

In Bezug auf die Verwendung von Mobiltelefonen in der Schule gibt es immer noch einige Kontroversen. Einige Eltern und Lehrer sind der Meinung, dass die Handynutzung in der Schule zu Ablenkung und Unordnung führen kann. Andere argumentieren jedoch, dass es einen gewissen Nutzen haben könnte, wenn Schüler während des Unterrichts ihr Handy einsetzen.

Viele Eltern sind besorgt, dass ihre Kinder beim Spielen mit dem Handy während des Unterrichts abgelenkt werden können. Es ist nicht ungewöhnlich, dass Schüler sich beim Spielen mit dem Handy im Klassenzimmer unruhig verhalten oder andere Schüler ablenken. Auch Cyber-Mobbing ist ein weiteres Problem, das bei der Verwendung von Mobiltelefonen in der Schule auftreten kann.

Auf der anderen Seite argumentieren manche Leute, dass die Nutzung des Smartphones in der Schule für die Schüler sehr hilfreich sein kann. Da viele Handys zu Bruch gehen sollten Handyhüllen genutzt werden. Smartphones bieten den Schülern Zugriff auf eine Vielzahl von Informationen und ermöglichen es ihnen, neue Fähigkeiten zu erwerben und zu lernen. Mit Hilfe von Apps und Websites können sich Schüler auf Prüfungen vorbereiten und über Forschungsarbeit informieren. Haben Sie in ein hochwertiges Gerät für Ihr Kind investiert, sollten Sie es schützen, beispielsweise mit einem Cover für iphone 12 Hüllen.

Es ist schwer zu entscheiden, ob die Nutzung des Mobiltelefons in der Schule gut oder schlecht ist. Wir müssen uns jedoch fragen, welchen Nutzen die Verwendung dieser Technologie für unsere Kinder hat. Wenn wir uns diese Frage stellen, können wir uns vielleicht eine fundierte Meinung zur Handynutzung in der Schule bilden. In jedem Fall sollten klare Regeln kommuniziert werden und ein einheitliches Konzept für den Umgang mit Smartphones im Schulbetrieb entworfen werden.

Regeln für eine sichere, effiziente und produktive Handynutzung an Schulen

Es ist völlig verständlich, dass Schüler auf ihre Handys zugreifen möchten. Dank der modernen Technologie und den unzähligen Funktionen, die sie bietet, kann das Handy ein wertvolles Werkzeug sein. Es kann Schülern helfen, ihre Schulaufgaben zu erledigen, Verbindungen zu knüpfen und sogar beim Lernen zu helfen. Daher ist es wichtig, dass Schulen Richtlinien festlegen, die eine sichere, effiziente und produktive Nutzung von Handys an ihren Schulstandorten ermöglichen.

Zunächst sollten Schulleiter eindeutige Regeln für die Nutzung von Handys in der Schule erlassen. Dies kann beispielsweise bestimmen, welcher Zeitraum als akzeptabel angesehen wird – zum Beispiel nur in den Pausen oder nur in bestimmten Fächern – und welche Art von Aktivitäten verboten sind (wie z.B. das Ansehen von Videos oder das Spielen von Spielen). Die Regeln müssen auch verbindlich sein: Wenn jemand gegen diese Regeln verstößt, sollte es Konsequenzen geben – beispielsweise eine Verwarnung oder gar die Beschlagnahme des Geräts für einen bestimmten Zeitraum.

Darüber hinaus sollten Lehrer regelmäßig überprüfen, ob die Schüler die Regeln befolgen. Auf diese Weise können sie Störungsverhalten frühzeitig erkennen und entsprechend reagieren. Das bedeutet nicht, dass Lehrer jedes Mal überprüfen müssen, wenn ein Student sein Handy benutzt. In Situationen mit hoher Aktivität ist es jedoch ratsam, dass Lehrer regelmäßig überprüfen und sicherstellen können, dass die Regeln befolgt werden.

Abschließend muss noch gesagt werden, dass es völlig in Ordnung ist für Schulkinder oder Jugendliche, ihr Handy an der Schule zu nutzen – solange es im Einklang mit den Richtlinien der jeweiligen Institution steht und nicht ablenkt oder stört. Mit den richtigen Richtlinien kann die mobile Technologie für alle Beteiligten ein positives Erlebnis sein – und damit auch zur Verbesserung des Lernerlebnisses beitragen!

Kleine, handliche Spielkarten können überall mithin genommen werden. Daher werden Kartenspiele gern auf Reisen oder im Park genutzt. Es gibt eine Vielzahl unterschiedlicher Spiele, einige Klassiker kennt jedoch fast jeder. Die äußerst beliebten Kartenspiele Blackjack und Poker werden auch in Casinos angeboten.

Die beliebtesten und bekanntesten Kartenspiele

Blackjack

Das berühmte Kartenspiel ist nahezu weltweit bekannt und bedient sich internationaler Regeln. Es ist einfach zu erlernen und bietet sich daher auch für Anfänger an. Schon bei Kindern ist der Klassiker unter „17+4“ bekannt. Vor rund vierhundert Jahren nannten Spieler das Kartenspiel „21“. Da jedoch amerikanische Casinos die Sonderregel einführten, dass eine extra Zahlung durch einen schwarzen Buben und ein Pik-Ass gewährt wird, trägt es heute den Titel Blackjack.

Um Blackjack zu spielen, wird ein französisches Blatt mit 52 Karten benötigt. Es kann zu zweit, aber auch mit mehreren Mitstreitern gespielt werden. Zunächst erhält jeder Mitspieler zwei verdeckte Karten. Je nachdem, wie nah die Blätter an dem Wert 21 sind, werden weitere Karten gezogen oder nicht. Wer mit seinen Karten möglichst nahe an dem Wert ist oder direkt 21 Punkte hat, der gewinnt die Runde. Wer Karten in der Hand hält, die über dem Wert sind, hat verloren.

Poker

Von Poker hat bestimmt schon fast jeder Mensch gehört. Zunächst wirkt das Kartenspiel ziemlich kompliziert, da oft von Poker Face, Strategien und verschiedenen Arten geredet wird. Dabei ist es gar nicht so schwer zu erlernen und ein unterhaltsamer Zeitvertreib. Sogar Meisterschaften werden in Poker ausgetragen, da es sich bei Poker nicht um ein reines Glücksspiel handelt. Mit guter Strategie können die Gewinnchancen gesteigert werden.

Historiker behaupten, dass Poker schon vor 1.000 Jahren in vielen Kulturen und auf mehreren Kontinenten bekannt war. Einige davon vertreten die Meinung, dass Poker von dem persischen Spiel „As Nas“ aus dem 16. Jahrhundert stammt. Sicher ist, dass es dem Kartenspiel „Poque“ gleicht, das damals schon gern mit Bluffen gespielt wurde.

Es gibt mittlerweile zahlreiche Varianten, die bekannteste ist Poker mit Texas Hold’em Regeln. Es beginnt, indem jeder Mitspieler zwei zufällige Karten erhält. Drei weitere Blätter werden in der Mitte offen hingelegt. Ziel des Spiels ist, eine möglichst gute Kombination mit den eigenen und den offenen Karten zu erhalten.

Wer denkt, er könnte eine gute Kombination erzielen, setzt einen Einsatz, bevor die vierte Karte in der Mitte offengelegt wird. Erhöht ein Mitstreiter den Einsatz, müssen die anderen Spieler den gleichen oder noch höheren Betrag setzen. Anschließend wird die fünfte und letzte Karte in der Mitte aufgedeckt und es folgen noch einmal Einsätze. Wer zum Schluss die beste Kombination besitzt, gewinnt die Runde.

Es gibt aber auch viele weitere Varianten, die zu Hause oder im Casino gespielt werden können. Die Kombinationen wie kleine und große Straße, Royal Flush usw. sind immer gleich, daher ist Poker gar nicht so schwer, wie die meisten Menschen denken.

Baccarat

Das Kartenspiel soll im 15. Jahrhundert erfunden worden sein und seinen Ursprung in Italien haben. Der Titel Baccara oder Baccarat steht für die Ziffer Null. Damals bediente sich das Spiel etwas anderer Regeln als heute.

Heute werden jedem Spieler zunächst zwei Karten übergeben. Besitzen diese eine Wertigkeit von acht oder neun, muss dies bekannt gegeben werden. Wurden die Zahlen noch nicht erreicht, kann der Kartenspieler entscheiden, noch ein weiteres Blatt aufzunehmen, das dann offengelegt wird.

Wurde eine dritte Karte gezogen, so muss auch der Mitspieler ein weiteres Blatt nehmen. Dann werden die Karten aufgedeckt und wer den höheren Wert besitzt, gewinnt die Runde.

Auch Baccarat gibt es in mehreren Variationen. Es beginnt jedoch immer mit zwei Karten, die ausgegeben werden. Die höchste Hand beträgt bei allen Baccarat-Arten einen Wert von 9 und die niedrigste 0. Wer die Grundregeln beherrscht, kann sich mit weiteren Variationen beschäftigen, um das bevorzugte Spiel zu finden.

Kartenspiele stationär oder im Online Casino nutzen

Stationäre Casinos und Glücksspielbetreiber im Internet bieten Kartenspiele an. Online kursieren zahlreiche Strategien, die für gesteigerte Gewinnchancen sorgen. Um diese gratis auszutesten, sollten Spieler zunächst Webseiten besuchen, die Kartenspiele ohne Echtgeld anbieten. Oft ist für das kostenlose Kartenspiel nicht einmal eine Registrierung notwendig.

Auch andere Varianten von Poker, Blackjack oder Baccarat können ausgetestet werden. Wer sein Glück mit echten Geldeinsätzen ausprobieren möchte, kann einen stationären Betreiber besuchen und dort an einem der Tische Platz nehmen oder im Online Casino spielen. Im Internet haben Spieler den Vorteil, dass es viele Bonusangebote gibt, wodurch schon mit kleinen Investitionen lange und oft gespielt werden kann. Außerdem sind die Einsatzlimits in Internet Casinos kleiner. An vielen Online Tischen kann bereits ab 10 Cent Einsatz gespielt werden, während stationär meistens mindestens 2 Euro gesetzt werden müssen.

Spielautomaten begegnen uns überall. Sie sind längst nicht mehr ausschließlich in dunklen Spielotheken und Casinos zu finden, sondern versuchen uns auch in Kneipen und beim Imbiss um die Ecke mit ihren bunten Lichtern und verlockenden Klängen zu ein paar Einsätzen zu verführen. In noch größerer Anzahl gibt es sie jedoch in Online Casinos, wo die auch als Slots bezeichneten Automaten quasi immer den mit Abstand größten Teil des Spieleportfolios ausmachen. Auch auf vielen Informationsplattformen zum Thema Glücksspiel werden unzählige Spielautomaten vorgestellt.

Doch wie funktionieren Slots? Welchen Prinzipien folgen sie und wie viel Mathematik spielt bei der Entwicklung derartiger Games eine Rolle? Ist es vielleicht sogar möglich, durch das Verständnis der Funktionsweise von Automatenspielen zu mehr Gewinnen zu kommen? Wir werfen einen genaueren Blick auf die populären Münzschlucker und geben Antworten.

Der Zufallszahlengenerator

Zunächst einmal möchten wir mit einem Gerücht aufräumen, das sich in der Glücksspiel-Szene noch immer hartnäckig hält: Es existieren keine sogenannten “heißen” Slots, die kurz vor einer großen Auszahlung stehen, weil schon lange kein nennenswerter Gewinn mehr ausgeschüttet wurde. Umgekehrt sind demnach auch “kalte” Automaten, die gerade großzügig ausgezahlt haben und daher nun eine Weile keine Erlöse ausgeben werden, nicht mehr als ein Märchen. Ebenso unsinnig ist die Annahme, dass man zu bestimmten Tageszeiten bessere Gewinnchancen hat.

Jeder Spielautomat bildet seine Zeichenkombinationen auf den Walzen mit Hilfe eines Zufallszahlengenerators, der sich nicht um vorangegangene Gewinne schert. Er erzeugt bei jeder Drehung nach demselben Verfahren zufällige Zahlenfolgen, anhand derer die entsprechenden Symbole auf dem Spielfeld ermittelt werden.

Man unterscheidet zwischen nicht-deterministischen Zufallsgeneratoren, die auch bei identischen Ausgangsbedingungen stets unterschiedliche Zahlenreihen erzeugen, und deterministischen Zufallsgeneratoren, die bei gleichen Voraussetzungen immer dieselben Ergebnisse liefern. Bei der Entwicklung von Software wie Casinospielen werden deterministische RNGs (RNG – Random Number Generator) verwendet, die sogenannte Pseudo-Zufallszahlen liefern. Diese sehen zwar zufällig aus, sind es jedoch nicht wirklich, da sie durch einen reproduzierbaren Algorithmus berechnet werden. Für Glücksspiele sind auf diese Weise erzeugte Zahlenreihen jedoch absolut ausreichend, allerdings auch alternativlos, weil nicht-deterministische Zufallszahlengeneratoren durch eine Software nicht zu realisieren sind.

Die Auszahlungsquote

Kaum eine Kenngröße von Spielautomaten wird so häufig falsch definiert oder missinterpretiert wie die Auszahlungsquote. Die Auszahlungsquote wird oft auch unter dem Begriff RTP (Return to Player) angegeben und beschreibt, wie viel aller an einem Slot vorgenommenen Einsätze im Durchschnitt wieder an die Spieler ausgezahlt werden. Sie ist ein statistischer Wert, der in aufwendigen und langwierigen Verfahren ermittelt wird. Dafür werden über einen langen Zeitraum unzählige Einsätze simuliert, die anschließend zusammenaddiert und gegen die damit erzielten Gewinne gerechnet werden. Heraus kommt ein Wert, der unter 1 bzw. unter 100% liegt. Er hat nichts mit der Gewinnwahrscheinlichkeit zu tun.

Da die Auszahlungsquote über sehr viele simulierte Runden bestimmt wird, hat sie für einen Nutzer, der eine Session in einem Online Casino spielt, kaum Aussagekraft. Es würde auch keinen Sinn ergeben, in einen Spielautomaten zu investieren, wenn man bei einer Auszahlungsquote von beispielsweise 96% von vornherein weiß, dass man auf jeden Fall 4% seines Geldes verlieren wird. Jeder weiß, dass man das eine Mal Glück haben und mit einem Plus aus dem Spiel aussteigen kann, während es bei einem anderen Mal einfach nicht läuft. Die Auszahlungsquote kann aber als Vergleichsgröße gegenüber anderen Slots hergenommen werden. Je höher der RTP-Wert eines Automaten, desto besser zahlt er grundsätzlich aus.

Für das Gegenteil der Auszahlungsquote gibt es übrigens auch einen Begriff. Jeder dürfte schon einmal davon gehört haben – es handelt sich nämlich um den Hausvorteil. Er beschreibt, welcher Anteil aller riskierten Einsätze durchschnittlich im Casino verbleiben.

Die Volatilität

Wie hoch die Gewinnwahrscheinlichkeit bei einem Automatenspiel ist, darüber gibt der Hersteller keine Auskunft. Fakt ist jedoch, dass sie unter anderem von der Anzahl der Walzen, der Reihen und der unterschiedlichen Symbole abhängig ist. Es gibt allerdings eine andere Größe, die von den Entwicklern bekanntgegeben wird. Die Rede ist von der Volatilität, bisweilen wird auch von Varianz gesprochen. Sie wird recht ungenau mit “niedrig”, “mittel” oder “hoch” angegeben.

Mit der Volatilität wird eine Aussage darüber getroffen, wie häufig und wie hoch ein Spielautomat auszahlt. Ein Slot mit hoher Volatilität zahlt verhältnismäßig selten, dafür aber größere Gewinne aus. Man benötigt also sowohl Geduld als auch ein belastbares Budget, um längere Durststrecken ohne nennenswerte Erlöse überstehen zu können. Bei einem Automaten mit niedriger Varianz hingegen kommt es häufiger zu Auszahlungen, die dafür aber geringer ausfallen. Derartige Slots eignen sich besonders gut für Anfänger bzw. Spieler mit weniger dicker Brieftasche.

Viel Mathematik, doch nur hinter den Kulissen

Slots sind komplexe Software-Konstrukte, bei denen sich die Entwickler der Mathematik bedienen, um den Spielausgang in die gewünschte Richtung zu lenken. Allerdings lassen sich die Hersteller nicht in die Karten schauen, welche Algorithmen dafür genutzt werden. Für den Spieler ist das auch gar nicht wichtig. Er bekommt mit der Auszahlungsquote und der Volatilität eine grobe Aussage darüber, mit was für einem Automaten er es zu tun hat. Ob er tatsächlich etwas gewinnen wird, darüber entscheidet letztendlich nur sein Glück.

Chemie und Mathematik sind zwei der Grundlagenwissenschaften, auf denen unsere moderne Gesellschaft fußt. Ohne sie wäre unser Leben undenkbar! Viele Menschen haben Angst vor Chemie und Mathematik. Dabei sind beide Fächer gar nicht so schwer, wie viele denken! Wir erklären euch, warum Chemie und Mathematik so wichtig für unseren Alltag sind. Auch Mathematik ist überall um uns herum – auch wenn man es oft gar nicht merkt. Viele Menschen haben Angst vor dem Fach, weil sie denken, es sei zu kompliziert. Doch das stimmt absolut nicht! In diesem Blog-Post erklären wir euch ganz genau, warum Mathematik so wichtig für unseren Alltag ist und warum ihr keine Angst davor haben müsst!

Die Bedeutung von Chemie in unserem täglichen Leben

Chemie ist allgegenwärtig und beeinflusst unser tägliches Leben auf vielfältige Weise. Zu den Produkten, die wir dank der Chemie nutzen können, gehören zum Beispiel Medikamente, Kosmetika, Lebensmittel und Reinigungsmittel. Auch viele Materialien wie etwa Kunststoffe und Textilien sind ohne die chemische Industrie nicht denkbar.

Doch Chemie ist nicht nur in unserer materiellen Umwelt präsent, sondern auch in unserem Körper. Jede Zelle besteht aus chemischen Substanzen, und auch unsere DNA ist ein komplexes chemisches Molekül. Wir atmen Sauerstoff ein, um Energie für unseren Körper zu produzieren – ein Prozess, bei dem chemische Reaktionen ablaufen.

Auch unsere Gedanken sind chemisch bedingt: Die Neurotransmitter im Gehirn steuern unsere Stimmung und unser Verhalten. Kommt es zu einem Ungleichgewicht dieser Botenstoffe, kann es zu psychischen Erkrankungen wie Depressionen oder ADHS kommen.

All diese Beispiele zeigen, wie sehr Chemie unser Leben beeinflusst. Ohne sie wäre ein modernes Leben in unserer heutigen Gesellschaft nicht möglich.

Wie wichtig ist Mathematik für unser tägliches Leben?

Mathematik ist eine Schlüsselwissenschaft, die uns hilft, die Welt um uns herum zu verstehen. Ob wir es merken oder nicht, wir gebrauchen sie jeden Tag – beim Einkaufen, beim Autofahren oder sogar beim Kochen.

Natürlich können wir auch ohne Mathematik leben, aber unser Leben wäre sehr viel schwieriger und weniger bequem. Stellen Sie sich zum Beispiel vor, Sie müssten Ihr Auto selbst reparieren, ohne Zugriff auf technische Daten und Anleitungen. Oder versuchen Sie mal, ein neues Rezept auszuprobieren, ohne die Zutaten abzuwiegen oder die Garzeit einzuhalten. In beiden Fällen wäre es sehr viel schwieriger, ohne Mathematik zurechtzukommen.

Deshalb ist es wichtig, dass wir uns mit Mathematik auseinandersetzen und sie verstehen lernen. Auch wenn wir sie nicht immer bewusst nutzen, so hilft sie uns doch dabei, unseren Alltag besser zu meistern.

Warum können wir ohne Chemie und Mathematik nicht leben?

Wenn wir uns die Welt um uns herum anschauen, ist es offensichtlich, dass Chemie und Mathematik überall zu finden sind. Chemie ist die Wissenschaft, die die Elemente und ihre Reaktionen untersucht. Mathematik ist die Wissenschaft der Zahlen und der Berechnungen. Beide sind unerlässlich für unseren Alltag.

Chemie ist in allem, was wir tun, präsent. Ob wir essen, trinken, atmen oder schlafen – überall finden chemische Reaktionen statt. Die Luft, die wir einatmen, besteht aus Sauerstoff und Stickstoff. Diese beiden Elemente reagieren miteinander und bilden das Gas Stickstoffdioxid. Dieses Gas ist giftig und kann zu Atemnot führen. Wenn wir essen, nehmen wir Nährstoffe auf, die unseren Körper braucht, um zu funktionieren. Diese Nährstoffe werden in unserem Magen-Darm-Trakt chemisch verarbeitet und in energiereiche Moleküle umgewandelt. Ohne Chemie könnten wir also nicht leben.

Auch Mathematik ist allgegenwärtig. Jedes Mal, wenn wir etwas kaufen, müssen wir rechnen. Wir müssen herausfinden, ob wir genug Geld haben und ob der Preis fair ist. Auch beim Kochen oder Backen müssen wir oft exakte Mengenangaben einhalten, damit das Essen gut gelingt. Auch Verkehrsteilnehmer müssen sich ständig mit Zahlen auseinandersetzen: Sie müssen Geschwindigkeiten berechnen und Abstände einschätzen. Ohne Mathematik könnte unsere moderne Gesellschaft nicht funktionieren.

Periodensystem und Grundrechenarten

Wir können uns das Periodensystem als eine Tabelle vorstellen, in der die verschiedenen Elemente angeordnet sind. Auf diese Weise können wir sehen, welche Elemente miteinander verbunden sind und wie sie aufeinander wirken. Die meisten Menschen denken jedoch nicht darüber nach, wie dieses System entstanden ist oder warum es so wichtig ist.

Das Periodensystem der Elemente entstand aus dem Bedarf heraus, die chemischen Elemente zu ordnen und zu verstehen, wie sie miteinander interagieren. Dies war keine einfache Aufgabe, denn zu Beginn gab es keine Möglichkeit, die Elemente direkt zu untersuchen. Stattdessen mussten Wissenschaftler sich auf Beobachtungen und Experimente verlassen.

Einer der ersten Wissenschaftler, die versuchten, das Periodensystem zu entwickeln, war Dmitri Mendeleev. Er beobachtete, dass, wenn man die Elemente nach ihrem Atomic Number (Anzahl der Protonen) ordnete, bestimmte Elemente ähnliche Eigenschaften hatten. Zum Beispiel hatten elemente mit den Atomic Numbers 3 (Lithium), 11 (Sodium) und 19 (Potassium) ähnliche Eigenschaften. Mendeleev entwickelte das Periodensystem weiter und ordnete die Elemente in Gruppen ein, die sogenannten „Periods“ (Zeiträume).

Heute ist das Periodensystem ein unverzichtbarer Bestandteil der Chemie und wird täglich von Wissenschaftlern und Studierenden genutzt. Es hilft uns, die Eigenschaften der verschiedenen Elemente zu verstehen und ermöglicht uns die Planung komplexer chemischer Reaktionen. Ohne das Periodensystem der Chemie wäre es nahezu unmöglich, unsere modernen Gesellschaften zu betreiben.

Fazit

Ohne Chemie und Mathematik können wir nicht leben. Diese beiden Fächer sind die Grundlage für so viele andere Bereiche unseres Lebens. Wir brauchen sie, um zu verstehen, wie die Welt um uns herum funktioniert. Wir brauchen sie, um komplexe Probleme zu lösen. Und wir brauchen sie, um neue Technologien und Innovationen zu entwickeln.

Die Wahrscheinlichkeitsrechnung ist ein wichtiges Instrument, um Risiken zu analysieren und zu minimieren. Doch was genau ist die Wahrscheinlichkeitsrechnung und wie kann sie angewendet werden?

Was ist eine Wahrscheinlichkeit?

Wahrscheinlichkeit ist die Häufigkeit, mit der ein bestimmtes Ereignis oder Ergebnis in einer Stichprobe oder beobachteten Serie auftritt. Wenn beispielsweise die Wahrscheinlichkeit eines Münzwurfes „Kopf“ beträgt, bedeutet dies, dass wir erwarten würden, ungefähr 50 Prozent der Würfe wären „Kopf“.

Einführung in die Wahrscheinlichkeitsrechnung

Die Wahrscheinlichkeitsrechnung ist ein wesentlicher Bestandteil der Statistik und ermöglicht es uns, mit probabilistischen Aussagen umzugehen. In diesem Artikel befassen wir uns zunächst mit den Grundlagen der Wahrscheinlichkeit und sehen uns an, wie sich die Wahrscheinlichkeit verändert, wenn bestimmte Ereignisse eintreten.

Die Wahrscheinlichkeit eines Ereignisses gibt an, wie wahrscheinlich es ist, dass dieses Ereignis eintritt. Man kann sie entweder als Bruch (z.B. 1/2) oder als Dezimalzahl (z.B. 0,5) angeben. Die Wahrscheinlichkeit eines Ereignisses liegt immer zwischen 0 und 1, wobei 0 bedeutet, dass das Ereignis mit Sicherheit nicht eintreten wird und 1 bedeutet, dass das Ereignis mit Sicherheit eintreten wird.
Wenn Sie beispielsweise einen Würfel rollen, gibt es sechs mögliche Ergebnisse: 1, 2, 3, 4, 5 oder 6. Jedes dieser Ergebnisse ist genauso wahrscheinlich, daher hat jedes eine Wahrscheinlichkeit von 1/6.

Wie wird sie berechnet?

Die Wahrscheinlichkeit eines Ereignisses berechnet man, indem man die Anzahl der möglichen Ergebnisse, in denen das Ereignis eintritt, durch die Anzahl aller möglichen Ergebnisse insgesamt dividiert.

Wahrscheinlichkeiten können dabei für verschiedene Ereignisse berechnet werden. Zum Beispiel kann die Wahrscheinlichkeit für das Auftreten eines bestimmten Ereignisses berechnet werden, aber auch die Wahrscheinlichkeit, dass zwei oder mehrere Ereignisse gleichzeitig stattfinden.

Die Berechnung von Wahrscheinlichkeiten basiert auf dem sogenannten Gesetz der großen Zahlen. Dieses Gesetz besagt, dass sich die tatsächlichen Ergebnisse einer zufälligen Veranstaltung mit der Zeit der Theorie annähern.

Das Gesetz der großen Zahlen ist ein wesentlicher Bestandteil der Wahrscheinlichkeitstheorie. Es besagt, dass sich die tatsächlichen Ergebnisse einer zufälligen Veranstaltung mit der Zeit der Theorie annähern. Dieses Gesetz ist sehr nützlich, um zu bestimmen, wie wahrscheinlich es ist, dass ein bestimmtes Ereignis eintritt. Beispielsweise kann es helfen, die Wahrscheinlichkeit zu berechnen, dass ein bestimmter Würfel beim nächsten Wurf eine Sechs zeigt.

Chi-Quadrat-Test

Der Chi-Quadrat-Test ist ein Test, der verwendet wird, um festzustellen, ob zwei Variablen miteinander verbunden sind. Es gibt verschiedene Arten von Chi-Quadrat-Tests, aber der häufigste ist der unabhängige Chi-Quadrat-Test. Dieser Test wird durchgeführt, um festzustellen, ob es einen Unterschied zwischen zwei Gruppen gibt, zum Beispiel Männer und Frauen oder Jungen und Mädchen.

Der Chi-Quadrat-Test funktioniert, indem er die Anzahl der Beobachtungen in jeder Gruppe mit den erwarteten Anzahl der Beobachtungen vergleicht. Wenn die Anzahl der Beobachtungen in einer Gruppe deutlich von den erwarteten Anzahl abweicht, bedeutet dies, dass es einen Unterschied zwischen den beiden Gruppen gibt.

Anwendungsbeispiele der Wahrscheinlichkeitsrechnung

Die Wahrscheinlichkeitsrechnung ist ein wichtiges Werkzeug in der Statistik. Viele statistische Testverfahren, wie zum Beispiel der oben beschriebene Chi-Quadrat-Test, basieren auf den Gesetzen der Wahrscheinlichkeit. Auch die Regression, ein wichtiges Verfahren der Statistik, nutzt Wahrscheinlichkeitsrechnung.

Die Wahrscheinlichkeitsrechnung hat in vielen Bereichen der Mathematik und Physik Anwendung gefunden. In diesem Abschnitt sollen einige Beispiele dafür vorgestellt werden.

Finanzmathematik

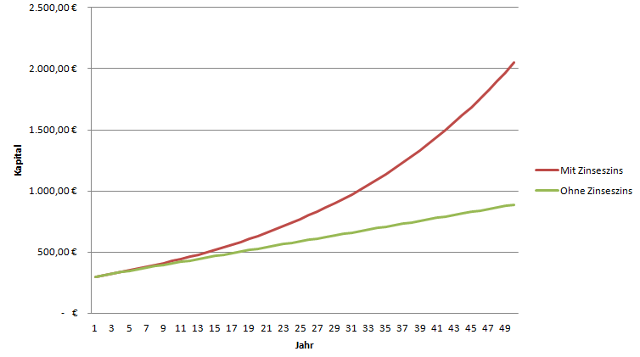
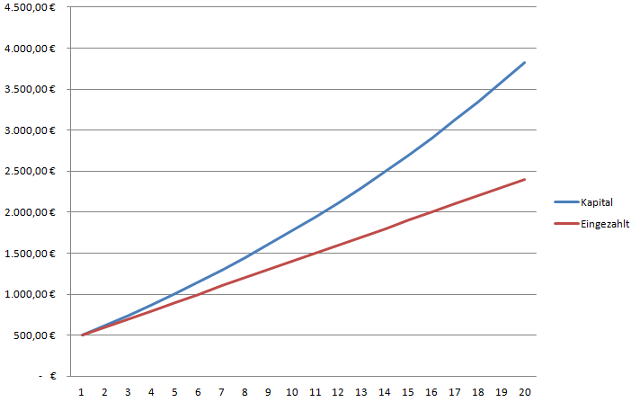
In der Finanzmathematik kommt die Wahrscheinlichkeitsrechnung bei der Berechnung von Renditen und Risiken zum Einsatz. Auch beim Börsenhandel wird sie verwendet, um die Wahrscheinlichkeit von Kursentwicklungen zu berechnen.

Roulette Wahrscheinlichkeiten

In der Spielbank oder im Online Casino kann man ebenfalls mit Wahrscheinlichkeiten rechnen. Beispielsweise spricht man beim European bzw. French Roulette von einem RTP-Wert von 97,30% sowie beim American Roulette von 94,74%. Diese Quote gibt an, dass der eingezahlte Betrag bei der Auszahlung über einen längeren Zeitraum mit dieser Wahrscheinlichkeit ausgezahlt wird. Der Unterschied dieser Roulette Wahrscheinlichkeiten wird durch das zweite Zahlenfach 0 bei der amerikanischen Variante begründet. Bei diesem Kesselspiel kann man zudem selbst großen Einfluss auf die Gewinnchance nehmen. Es macht nämlich einen großen Unterschied, ob man auf eine bestimmte Zahl setzt, auf eine Zahlengruppe oder auf Rot/Schwarz bzw. Gerade/Ungerade. Der Bereich rund um Roulette ist bis in kleinste Detail analysiert. Sehr gut zu erkennen ist das in diesem Guide zu Roulette Wahrscheinlichkeiten.

Spiele

Beim Pokern rechnen viele Spieler grob die Wahrscheinlichkeiten aus. Die kann zum Beispiel beim Poker passieren, um seine Chancen besser abzuschätzen. Der Großteil der Spieler verlässt sich aber lieber auf sein Glück und hofft auf einen großen Gewinn.

Physik

In der Physik wird die Wahrscheinlichkeitsrechnung bei der Berechnung von Messfehlern eingesetzt. Sie kann auch dazu verwendet werden, die Wahrscheinlichkeit für bestimmte physikalische Vorgänge zu berechnen, zum Beispiel für die Zerfallszeit eines radioaktiven Isotops.

Wartungsintervalle von Maschinen

Wartungsintervalle von Maschinen sind ein wichtiges Thema in der Instandhaltung. Die Wahl des richtigen Intervalls ist entscheidend für die Effizienz der Instandhaltung und die Kosten der Produktion.

Wartungsintervalle werden in zwei Hauptkategorien unterteilt: Zeit-basierte Intervalle und Laufleistungs-basierte Intervalle. Zeit-basierte Intervalle werden häufig für routinemäßige Wartungsarbeiten ver wendet, wie z.B. das Ölwechseln in einem Fahrzeug. Laufleistungs-basierte Intervalle werden häufig für Arbeiten an Komponenten verwendet, die unter hoher Beanspruchung stehen, wie z.B. die Bremsen in einem Fahrzeug.

Laufleistungs-basierte Intervalle sind in der Regel kürzer als Zeit-basierte Intervalle, da sie sich auf die tatsächliche Nutzung der Komponente beziehen und nicht auf die Zeit, die seit dem letzten Service vergangen ist.
Bei beidem hilft die Statistik den passenden Zeitpunkt zur Wartung / Ersatz zu finden bevor es zu einem Ausfall kommt.

Lustiges zur Wahrscheinlichkeitsrechnung

Es gibt eine ganze Reihe lustiger Zitate und Anekdoten rund um die Wahrscheinlichkeitsrechnung. Hier sind einige der besten:

„Die Wahrscheinlichkeit, dass etwas passiert, ist immer 1.“ – Murphy’s Law

„Wahrscheinlichkeit ist die Kunst, zu wissen, welche der zwei möglichen Dinge wahrscheinlicher ist.“ – Mark Twain

„Wenn etwas nicht passieren kann, wird es mit Sicherheit passieren.“ – Finagle’s Law

Wahrscheinlichkeitsrätsel – Urnenrätsel

Ein beliebtes Rätsel in der Wahrscheinlichkeitsrechnung ist das Urnenrätsel. Dabei geht es um zwei Urnen, die jeweils eine bestimmte Anzahl von Kugeln enthalten. In einer der Urnen befinden sich nur weiße Kugeln, in der anderen nur schwarze Kugeln. Nun wird eine der beiden Urnen ausgewählt und eine Kugel ohne Hinsehen herausgenommen. Die Frage ist nun, welche Wahrscheinlichkeit besteht, dass die gezogene Kugel aus der Urne mit den weißen Kugeln stammt?

Dieses Rätsel kann man mit Hilfe des Bayes -Theorem lösen. Die Wahrscheinlichkeit, dass die gezogene Kugel aus der Urne mit den weißen Kugeln stammt, ist also gleich der Wahrscheinlichkeit, dass die Urne mit den weißen Kugeln ausgewählt wurde, multipliziert mit der Wahrscheinlichkeit, dass eine weiße Kugel aus dieser Urne gezogen wird.

Fazit

Die Wahrscheinlichkeitsrechnung ist ein unverzichtbarer Bestandteil unserer modernen Welt. Denn ohne sie würden wir nicht in der Lage sein, zu verstehen und zu berechnen, was in unserer Welt passieren könnte.

Die Wahrscheinlichkeitsrechnung ermöglicht es uns, unsere Welt besser zu verstehen und zu gestalten. Denn sie hilft uns, die Dinge zu sehen, die wir sonst nicht sehen würden. Sie zeigt uns, welche Möglichkeiten wir haben und welche Konsequenzen unsere Handlungen haben können.

Die Wahrscheinlichkeitsrechnung ist also ein sehr mächtiges Werkzeug. Und mit ihrer Hilfe können wir unsere Welt verbessern.